题目内容

14．设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点，P为椭圆上任一点，点M的坐标为（6，4），则PM+PF1的最大值为15．

分析 由椭圆的定义可得：|PF1|+|PF2|=2a，可得|PM|+|PF1|=|PM|+2a-|PF2|≤10+|MF2|，即可得出．

解答 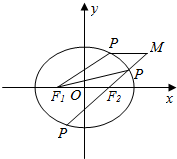解：如图所示，
由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1可得：a=5，b=4，c=$\sqrt{{a}^{2}-{b}^{2}}$=3．
∴F1（-3，0），F2（3，0），
由椭圆的定义可得：|PF1|+|PF2|=2a=10，
∴|PM|+|PF1|=|PM|+2a-|PF2|=10+（|PM|-|PF2|）≤10+|MF2|=10+$\sqrt{{3}^{2}+{4}^{2}}$=15，
则|PM|+|PF1|的最大值为15．
故答案为：15．

点评 本题考查了椭圆的标准方程及其性质、三角形三边大小关系、两点之间的距离公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．已知函数f（x）=log2（4x+1）-x．
（1）求证：函数f（x）是偶函数；
（2）若对任意x∈[1，2]，不等式f（x）≤log2（$\frac{m}{{2}^{x}}$+3）恒成立，求实数m的最小值；
（3）设函数g（x）=f（x）-log2（a•2x+1-4a）在（2，+∞）上有且只有一个零点，求正实数a．
5．函数y=loga（x2-ax+2）在[2，+∞）恒为正，则实数a的范围是（　　）
A．0＜a＜1B．1＜a＜2C．1＜a＜$\frac{5}{2}$D．2＜a＜3
2．已知函数f（x）=|lgx|，若$f（a）=f（b）=2f（\frac{a+b}{2}）（0＜a＜b）$，则b所在区间为（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
9．已知F1，F2为椭圆C：$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的左、右焦点，点E是椭圆C上的动点，$\overrightarrow{EF}$1•$\overrightarrow{EF}$2的最大值、最小值分别为（　　）
A．9，7B．8，7C．9，8D．17，8
19．已知椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），P是椭圆上非x轴上的一点，△PF1F2中，若F2（右焦点）关于∠F1PF2的外角平分线的对称点Q，则点Q的轨迹是（　　）
A．椭圆B．圆C．抛物线D．线段
6．若函数f（x）=x3-（$\frac{1}{2}$）x的零点在区间（n-1，n）内，则整数n=1．
3．一个几何体的三视图如图所示，则这个几何体的表面积等于10+2$\sqrt{3}$+4$\sqrt{2}$．
4．设实数x、y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$，则z=|x+y+4|的取值范围为[6，11]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网