题目内容
4.设实数x、y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$,则z=|x+y+4|的取值范围为[6,11].分析 根据题意,画出可行域,求出最优解,计算z=|x+y+4|的最小值与最大值即可.
解答 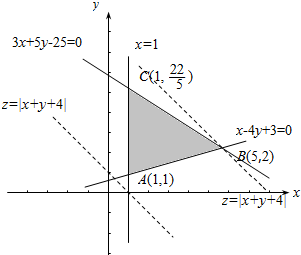 解:根据题意,实数x、y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$,
解:根据题意,实数x、y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$,
画出可行域,如图所示;
求出最优解,
则当x=1,y=1时,z=|x+y+4|取得最小值zmin=1+1+4=6,
当x=5,y=2时,z=|x+y+4|取得最大值zmax=5+2+4=11;
∴z的取值范围是[6,11].
故答案为:[6,11].
点评 本题考查了线性规划的应用问题,解题时应根据线性约束条件画出可行域,求出最优解,从而求出目标函数的取值范围,是基础题目.

练习册系列答案
相关题目
14.设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则PM+PF1的最大值为15.
12.已知数列{an}满足a1=1,an•an+1=2n,则$\frac{{{a_{2016}}}}{{{a_{2015}}}}$=( )
| A. | 2 | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{1}{2}$ |
19.点P(1,2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2 |
13.已知函数f(x)=sin2x,为了得到g(x)=cos2x的图象,只要将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |