题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)已知某班共有![]() 人,记这
人,记这![]() 人生日至少有两人相同的概率为
人生日至少有两人相同的概率为![]() ,
,![]() ,将一年看作365天.
,将一年看作365天.
(i)求![]() 的表达式;
的表达式;
(ii)估计![]() 的近似值(精确到0.01).
的近似值(精确到0.01).
参考数值:![]() ,
,![]() ,
,![]() .
.
【答案】(1) ![]() (2) (i)
(2) (i)![]() (ii)
(ii)![]()
【解析】
(1)先讨论![]() 取不同范围内的值时函数的定义域,并根据函数值判断出
取不同范围内的值时函数的定义域,并根据函数值判断出![]() 是
是![]() 的极小值点。通过极值点处
的极小值点。通过极值点处![]() ,求得导函数代入即可求得
,求得导函数代入即可求得![]() 的值。求出
的值。求出![]() 的值后,再代回函数
的值后,再代回函数![]() ,证明
,证明![]() 即可。
即可。
(2)每个人生日都不同的概率为![]() ,所以根据对立事件的概率即可求得至少有两个人生日相同的概率。
,所以根据对立事件的概率即可求得至少有两个人生日相同的概率。
将![]() 代入i中得到的式子,可得
代入i中得到的式子,可得![]() ,令
,令![]() ,左右同取对数则
,左右同取对数则![]() ,进而可得t的范围,结合参考数据可求得
,进而可得t的范围,结合参考数据可求得![]() 的近似值。
的近似值。
(1)由题得,当![]() 时,
时,![]() 的定义域为
的定义域为![]() ;
;
当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 是
是![]() 的极小值点,故
的极小值点,故![]() .
.
而![]() ,于是
,于是![]() ,解得
,解得![]() .
.
下面证明当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() 符合题意.
符合题意.
综上,![]() .
.
(2)(i)由于![]() 人生日都不相同的概率为
人生日都不相同的概率为![]() ,
,
故![]() 人生日至少有两人相同的概率为
人生日至少有两人相同的概率为![]() .
.
(ii)由(1)可得当![]() 时,
时,![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
由(i)得![]()
![]() .
.
记![]() ,
,
则![]()
![]()
![]() ,
,
即![]()
由参考数值得![]()
于是![]()
故![]() .
.

【题目】某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.下图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
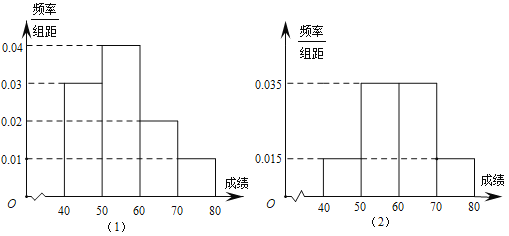
(1)请计算高一年级和高二年级成绩小于60分的人数;
(2)完成下面![]() 列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
列联表,并回答:有多大的把握可以认为“学生所在的年级与消防常识的了解存在相关性”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
高一 | |||
高二 | |||
合计 |
附:临界值表及参考公式:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |