题目内容
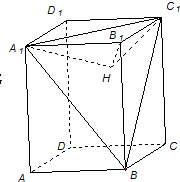 在长方体ABCD-A1B1C1D1中,AB=BC=3,BB1=4,B1H⊥平面A1BC1,垂足为H.
在长方体ABCD-A1B1C1D1中,AB=BC=3,BB1=4,B1H⊥平面A1BC1,垂足为H.(Ⅰ) 求证:H为△A1BC1的垂心;
(Ⅱ)求证:S2△A1B1C1=S△A1HC1•S△A1BC1(其中S△A1B1C1、S△A1HC1、S△A1BC1分别表示△A1B1C1,△A1HC1,△A1BC1的面积)
分析:(Ⅰ)证明BC1⊥平面A1BC1,可得BC1⊥A1H,同理C1H⊥A1B,故可证H为△A1BC1的垂心;
(Ⅱ)连接BH,并延长交A1C1于E,连接B1E,则由射影定理可得B1E2=EH×EB,由此可证结论.
(Ⅱ)连接BH,并延长交A1C1于E,连接B1E,则由射影定理可得B1E2=EH×EB,由此可证结论.
解答:证明:(Ⅰ)∵B1H⊥平面A1BC1,BC1?平面A1BC1,∴B1H⊥BC1,
∵长方体ABCD-A1B1C1D1中,A1B1⊥平面BC1,∴A1B1⊥BC1,
∵B1H∩A1B1=B1,∴BC1⊥平面A1B1H,∴BC1⊥A1H,
同理C1H⊥A1B
∴H为△A1BC1的垂心;
(Ⅱ)如图,连接BH,并延长交A1C1于E,连接B1E,

则由射影定理可得B1E2=EH×EB
∴
(A1C1)2B1E2=
A1C1×EH×
A1C1×EB
∴S2△A1B1C1=S△A1HC1•S△A1BC1.
∵长方体ABCD-A1B1C1D1中,A1B1⊥平面BC1,∴A1B1⊥BC1,
∵B1H∩A1B1=B1,∴BC1⊥平面A1B1H,∴BC1⊥A1H,
同理C1H⊥A1B
∴H为△A1BC1的垂心;
(Ⅱ)如图,连接BH,并延长交A1C1于E,连接B1E,

则由射影定理可得B1E2=EH×EB
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S2△A1B1C1=S△A1HC1•S△A1BC1.
点评:本题考查线面垂直,考查射影定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.