题目内容
在锐角△ABC中，角A，B，C所对边分别为a，b，c，已知sinA=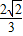
．（Ⅰ）求tan2
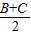的值；（Ⅱ）若a=2，S△ABC=
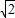，求b的值．
【答案】分析：（Ⅰ）通过同角三角函数的基本关系式，求出cosA，直接利用半角的正切公式求解tan2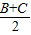
的值．
（Ⅱ）通过面积公式，以及余弦定理，求出b，c的关系，然后解方程组求解b的值即可．
解答：解：（Ⅰ）在锐角△ABC中，sinA=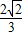
．则cosA=
，
所以tan2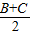
=
=
=
．
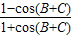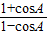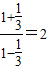（Ⅱ）由a=2，S△ABC=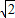
，可得
bcsinA=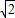
，所以bc=3，
由余弦定理b2+c2-2bccosA=a2，得，b2+c2=6，又bc=3，所以b=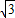
．
点评：本题考查余弦定理的应用，半角的三角函数公式的应用，考查转化思想，计算能力．
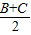的值．（Ⅱ）通过面积公式，以及余弦定理，求出b，c的关系，然后解方程组求解b的值即可．
解答：解：（Ⅰ）在锐角△ABC中，sinA=
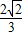．则cosA=，所以tan2
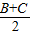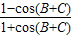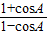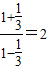===．（Ⅱ）由a=2，S△ABC=
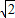，可得bcsinA=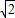，所以bc=3，由余弦定理b2+c2-2bccosA=a2，得，b2+c2=6，又bc=3，所以b=
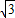．点评：本题考查余弦定理的应用，半角的三角函数公式的应用，考查转化思想，计算能力．
练习册系列答案
相关题目