题目内容
在抛物线![]()
![]() 上找一点P
上找一点P![]() ,其中
,其中![]() ,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C;
解析:
由于![]() ,因此过点P
,因此过点P![]() 的切线方程为
的切线方程为![]() ,该切线与
,该切线与![]() ,
,![]() 轴的交点分别是
轴的交点分别是![]() ,
,![]() .
.
所求面积A=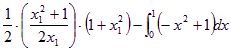 =
=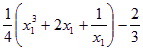
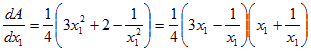 .
.
令![]() .(由于
.(由于![]() )得
)得![]() ,
,
由于此问题的最小值存在,且在![]() 内有唯一驻点,
内有唯一驻点,
故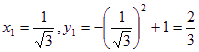 就是所求的点P,
就是所求的点P,
即:取切点为P![]() 时,所求的图形面积最小.
时,所求的图形面积最小.

练习册系列答案
相关题目
题目内容
在抛物线![]()
![]() 上找一点P
上找一点P![]() ,其中
,其中![]() ,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C;
由于![]() ,因此过点P
,因此过点P![]() 的切线方程为
的切线方程为![]() ,该切线与
,该切线与![]() ,
,![]() 轴的交点分别是
轴的交点分别是![]() ,
,![]() .
.
所求面积A=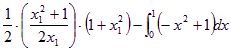 =
=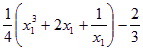
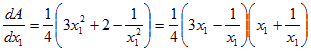 .
.
令![]() .(由于
.(由于![]() )得
)得![]() ,
,
由于此问题的最小值存在,且在![]() 内有唯一驻点,
内有唯一驻点,
故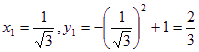 就是所求的点P,
就是所求的点P,
即:取切点为P![]() 时,所求的图形面积最小.
时,所求的图形面积最小.
