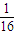题目内容
已知F是抛物线y 2=2Px (p>0)的焦点,若点M(2,![]() )恰好是直线MF被抛物线所截得弦的中点
)恰好是直线MF被抛物线所截得弦的中点
(1)求p的值及直线MF的方程
(2)能否在抛物线上找一点C ?使![]() . 若能,求出点C的坐标. 若不能,请说明理由.
. 若能,求出点C的坐标. 若不能,请说明理由.
(1)p=2,直线 MF 的方程为y= ![]() (x-1)(2)不存在点C满足题意
(x-1)(2)不存在点C满足题意
解析:
(1) (点差法) 设直线MF与抛物线交于A(x1 ,y1), B(x2 , y2), 又F(![]() ,0),
,0),
则y12=2px1 y22=2px2 ‚ …………2分
由‚- 得 (y2+y1) (y2-y1)=2p(x2-x1)
即 kAB(y2+y1)=2p ƒ
将kAB=kMF= ![]() , y1+y2=2
, y1+y2=2![]() 代人ƒ 解之有p=2
代人ƒ 解之有p=2
所以 kMF= ![]() , 直线 MF 的方程为y=
, 直线 MF 的方程为y= ![]() (x-1) …………7分
(x-1) …………7分
(2) 假设存在点C, 由(1)知y2=4x
设C(t2, 2t), 则 ![]() ,
, ![]() ,
,
由于![]()
可知![]() …………… 9分
…………… 9分
即 (t2-2)(t2—1)+(2t-![]() )(2t)=t4+t2-2
)(2t)=t4+t2-2![]() t+2=t4+(t-
t+2=t4+(t-![]() )2=0
)2=0
则t=0且t= ![]() ,故不存在点C满足题意 …………12分
,故不存在点C满足题意 …………12分

练习册系列答案
相关题目
已知F是抛物线y=
x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
| 1 |
| 4 |
A、x2=y-
| ||
B、x2=2y-
| ||
| C、x2=2y-1 | ||
| D、x2=2y-2 |
 x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )

 x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
x2的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )