题目内容
已知|PQ|=6，且点M到点P的距离是它到点Q的距离的
，求点M的轨迹方程．
| 1 | 5 |
分析：首先以PQ所在的直线为x轴，以其垂直平分线为y轴建立直角坐标系，设出M点的坐标后由题意列式，整理后即可得到答案．
解答：解：以PQ所在的直线为x轴，以其垂直平分线为y轴建立直角坐标系，
设点M的坐标为（x，y），则点P（-3，0），点Q（3，0），
由题意有：|MP|=
|MQ|，即
=
化简得点M的轨迹方程为：2x2+2y2+13x+18=0
设点M的坐标为（x，y），则点P（-3，0），点Q（3，0），
由题意有：|MP|=
| 1 |
| 5 |
| (x+3)2+y2 |
| 1 |
| 5 |
| (x-3)2+y2 |
化简得点M的轨迹方程为：2x2+2y2+13x+18=0
点评：本题考查了轨迹方程，考查了曲线方程的求法，是中低档题．
练习册系列答案
相关题目
．
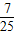=1(a＞0,b＞0)的左焦点，左准线l交x轴于点Q,点P是l上的一点,已知|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.
=λ
,当λ∈［6,+∞)时,求直线m的斜率k的取值范围.
．