题目内容
(12分)经过点P ,倾斜角为
,倾斜角为 的直线L与圆
的直线L与圆 相交于A、B两点。
相交于A、B两点。
(1)当P恰为AB的中点时,求直线AB的方程;
(2)当|AB|=8时,求直线AB的方程。
 ,倾斜角为
,倾斜角为 的直线L与圆
的直线L与圆 相交于A、B两点。
相交于A、B两点。(1)当P恰为AB的中点时,求直线AB的方程;
(2)当|AB|=8时,求直线AB的方程。
(1)  即:
即:
4x+2y+15="0(2)" 3x+4y+15=0或x=-3
 即:
即:4x+2y+15="0(2)" 3x+4y+15=0或x=-3
(1)先设出直线,然后再联立圆的方程,利用韦达定理求出倾斜角的正切值,即直线的斜率,从而求出直线AB的方程;(2)利用弦长公式列出关于倾斜角三角函数的等式,解方程求出直线的斜率,进一步求出直线的方程
解:(1)设直线L的方程为:
 (t为参数),代入x
(t为参数),代入x
(-3+tcos 整理得:
整理得: .
.
 依题意:
依题意: 即
即 的方程为:
的方程为: 即:
即:
4x+2y+15=0
(2)

依题意:
即:
由此得到:
 的方程为:
的方程为:
即:3x+4y+15=0. 时,x=-3
时,x=-3
 的方程为:3x+4y+15=0或x=-3
的方程为:3x+4y+15=0或x=-3
解:(1)设直线L的方程为:

 (t为参数),代入x
(t为参数),代入x
(-3+tcos
 整理得:
整理得: .
. 依题意:
依题意: 即
即 的方程为:
的方程为: 即:
即:4x+2y+15=0
(2)


依题意:

即:

由此得到:

 的方程为:
的方程为:
即:3x+4y+15=0.
 时,x=-3
时,x=-3 的方程为:3x+4y+15=0或x=-3
的方程为:3x+4y+15=0或x=-3
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,它们的夹角为
,它们的夹角为 ,如图所示,点C在以
,如图所示,点C在以 为圆心的圆弧AB上运动,若
为圆心的圆弧AB上运动,若 ,其中
,其中 ,则
,则 的最大值是 .
的最大值是 .
 的参数方程是( )
的参数方程是( ) (t为参数) B
(t为参数) B  (t为参数)
(t为参数)  (t为参数) D
(t为参数) D  (
( 为参数)
为参数)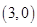 到直线
到直线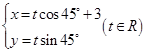 与直线
与直线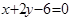 的交点Q的距离为
的交点Q的距离为 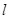 :
: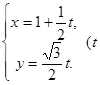 为参数), 曲线
为参数), 曲线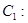
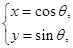 (
(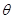 为参数).
为参数).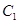 相交于
相交于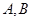 两点,求
两点,求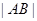 ;
;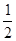 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的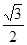 倍,得到曲线
倍,得到曲线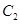 ,设点
,设点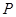 是曲线
是曲线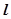 的距离的最小值.
的距离的最小值. (
( 为参数)的倾斜角
为参数)的倾斜角 等于( )
等于( ) ,所表示的曲线为( )
,所表示的曲线为( ) (t为参数)的斜率为 .
(t为参数)的斜率为 . )中,曲线
)中,曲线 与
与 的交点的极坐标为_____________
的交点的极坐标为_____________