题目内容
用半径为12cm，圆心角为90°的扇形纸片，围成一个圆锥的侧面，这个圆锥的底面半径为（ ）
| A、1.5cm | B、3cm | C、6cm | D、12cm |
分析：设圆锥的底面圆半径为r，根据圆锥的底面圆周长=扇形的弧长，解方程可得．
解答：解：设圆锥的底面圆半径为r，
∵圆锥的底面圆周长为扇形的弧长，
∴2πr=
×12，
解得r=3（cm）
故选B．
∵圆锥的底面圆周长为扇形的弧长，
∴2πr=
| π |
| 2 |
解得r=3（cm）
故选B．
点评：本题考查圆锥的计算．利用圆锥的底面圆周长为扇形的弧长是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在半径为R、圆心角为
如图，在半径为R、圆心角为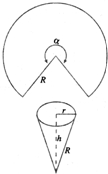
如图，用半径为R的圆铁皮，剪一个圆心角为α的扇形，制成一个圆锥形的漏斗，问圆心角α取什么值时，漏斗容积最大．（圆锥体积公式：