题目内容
已知x>0,y>0,求证: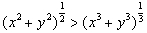 .
.
思路分析:利用乘方公式和不等式x2+y2≥2xy.
证法一:要证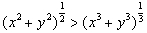 ,
,
只要证(x2+y2)3>(x3+y3)2,
即证x6+3x4y2+3x2y4+y6>x6+2x3y3+y6.
∵x>0,y>0,即证3x2+3y2>2xy.
∵3x2+3y2>x2+y2≥2xy,
即3x2+3y2>2xy.
∴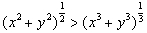 .
.
以上证法显然是分析法.
倒着写回去就是综合法.
证法二:由x>0,y>0,
∴3x2+3y2>x2+y2≥2xy,
即3(x2+y2)x2y2>2xy·x2y2.
∴3x4y2+3x2y4>2x3y3.
两边都加上x6+y6,得
x6+y6+3x4y2+3x2y4>x6+y6+2x3y3,
即(x2+y2)3>(x3+y3)2.
两边开6次方得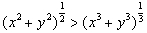 .
.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目