题目内容
9.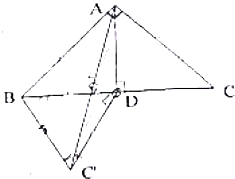 如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)
如图,在△ABC中,∠BAC=90°,AB=AC=2,AD⊥BC于D.将△ADC沿AD翻折至△ADC′,下列说法中正确的是①③④(写出所有正确命题的序号)①AD⊥BC′;
②BC′可能与平面△ADC′垂直;
③D-ABC′可能是正三棱锥;
④三棱锥D-ABC′体积的最大值为$\frac{\sqrt{2}}{3}$.
分析 根据已知结合线面垂直的判定定理和性质,可判断①②;结合正三棱锥的定义,要判断③;求出三棱锥D-ABC′体积的最大值,可判断④.
解答 解:∵AD⊥BD,AD⊥C′D,BD,C′D?平面BC′D,C′D∩BD=D,
∴AD⊥平面BC′D,
又∵BC′?平面BC′D,
∴AD⊥BC′,故①正确;
在△BC′D中,BD=C′D,
故∠BC′D不可能为直角,
即BC′⊥C′D不成立,
故BC′不可能与平面△ADC′垂直;
故②错误;
当BD⊥C′D时,D-ABC′是正三棱锥,
故③正确;
当BD⊥C′D时,三棱锥D-ABC′体积的最大值为$\frac{\sqrt{2}}{3}$.
故④正确;
故答案为:①③④.
点评 本题考查的知识点是棱锥的结构特征,线面垂直的判定与性质,难度中档.

练习册系列答案
相关题目
17.已知函数f(x)=2-x2,g(x)=x.若f(x)*g(x)=min{f(x),g(x)},那么,f(x)*g(x)的最大值是( )(注:min表示最小值)
| A. | 2 | B. | 1 | C. | 0 | D. | $-\frac{1}{2}$ |
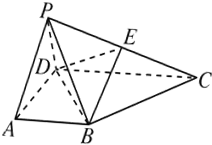 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.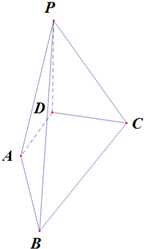 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.