题目内容
已知A={x|x2-ax+a2-19=0},B={x|x2-5x+8=2},C={x|x2+2x-8=0}.若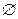
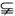 A∩B,且A∩C=
A∩B,且A∩C=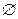 ,求a的值.
,求a的值.
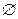
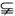 A∩B,且A∩C=
A∩B,且A∩C=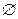 ,求a的值.
,求a的值.a=-2.
∵B={x|(x-3)(x-2)=0}={3,2},C={x|(x+4)(x-2)=0}={-4,2},又∵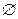
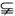 A∩B,∴A∩B≠
A∩B,∴A∩B≠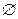 .
.
又∵A∩C=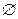 ,∴-4
,∴-4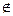 A,2
A,2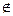 A,3∈A.∴由9-3a+a2-19=0,解得a=5或a=-2.
A,3∈A.∴由9-3a+a2-19=0,解得a=5或a=-2.
(1)当a=5时,A={2,3},此时A∩C={2}≠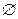 ,矛盾,∴a≠5;
,矛盾,∴a≠5;
(2)当a=-2时,A={-5,3},此时A∩C=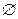 ,A∩B=
,A∩B= {3}≠
{3}≠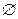 ,符合条件.
,符合条件.
综上(1)(2)知a="-2."
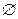
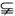 A∩B,∴A∩B≠
A∩B,∴A∩B≠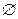 .
.又∵A∩C=
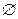 ,∴-4
,∴-4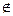 A,2
A,2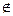 A,3∈A.∴由9-3a+a2-19=0,解得a=5或a=-2.
A,3∈A.∴由9-3a+a2-19=0,解得a=5或a=-2.(1)当a=5时,A={2,3},此时A∩C={2}≠
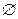 ,矛盾,∴a≠5;
,矛盾,∴a≠5;(2)当a=-2时,A={-5,3},此时A∩C=
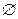 ,A∩B=
,A∩B= {3}≠
{3}≠ ,符合条件.
,符合条件.综上(1)(2)知a="-2."

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
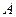 是空集,求
是空集,求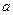 的取值范围;
的取值范围;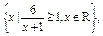 B=
B=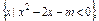
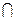 (
( RB);
RB);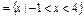 ,求实数m的值.
,求实数m的值.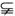 M
M M
M M
M M
M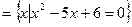 ,B=
,B=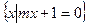 ,且
,且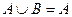 ,求实数
,求实数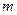 的值组成的集合。
的值组成的集合。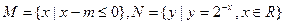 ,若
,若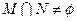 ,则实数m的取值范围是( )
,则实数m的取值范围是( )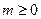
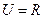 ,集合
,集合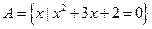 ,
,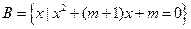 ;
;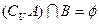 ,求
,求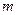 的值。
的值。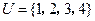 ,
,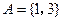 ,
,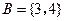 ,则CU
,则CU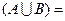 ( )
( )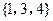
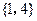
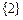
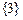
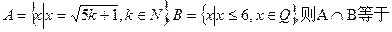 ( )
( ) B
B 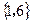 C
C 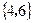 D
D