题目内容
已知A={x| },B={x|x2-4x-m≥0},若A⊆B,,则实数m的取值范围
},B={x|x2-4x-m≥0},若A⊆B,,则实数m的取值范围
- A.[0,+∞)
- B.(-∞,-3]
- C.[-3,0]
- D.(-∞,-3]∪[0,+∞)
B
分析:把集合A中的不等式移项右边变为0,左边通分后,转化为x+2与x-2异号,求出不等式的解集即可得到集合A,根据A⊆B,得到二次函数f(x)=x2-4x-m在区间(0,1)上恒正,即可求出、得结果.
解答:(1)由集合A中的不等式: ?
?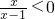 ?0<x<1,即A={x|0<x<1};
?0<x<1,即A={x|0<x<1};
∵A⊆B
∴令f(x)=x2-4x-m,则f(1)≤0,
即1-4-m≤0,解得m≤-3.
故选B.
点评:此题考查了一元二次不等式的解法,考查了两集合包含关系的应用,体现了转化的数学思想,是一道综合题.属中档题.
分析:把集合A中的不等式移项右边变为0,左边通分后,转化为x+2与x-2异号,求出不等式的解集即可得到集合A,根据A⊆B,得到二次函数f(x)=x2-4x-m在区间(0,1)上恒正,即可求出、得结果.
解答:(1)由集合A中的不等式:
 ?
?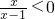 ?0<x<1,即A={x|0<x<1};
?0<x<1,即A={x|0<x<1};∵A⊆B
∴令f(x)=x2-4x-m,则f(1)≤0,
即1-4-m≤0,解得m≤-3.
故选B.
点评:此题考查了一元二次不等式的解法,考查了两集合包含关系的应用,体现了转化的数学思想,是一道综合题.属中档题.

练习册系列答案
相关题目
 },B={y|y=2x,x>0},则A×B=( )
},B={y|y=2x,x>0},则A×B=( ) },B={y|y=2x,x>0},则A×B=( )
},B={y|y=2x,x>0},则A×B=( )