题目内容
如图，在四面体 PABC中，E、F分别为CP、AB的中点，且EF=5，PB=8，AC=6则直线PB与直线AC所成角的大小为________．
90°
分析：取BC的中点G，连接EG，FG，由三角形的中位线定理，可得EG∥PB，FG∥AC，即∠EGF即为直线PB与直线AC所成角，根据EF=5，PB=8，AC=6，解三角形EFG，即可得到直线PB与直线AC所成角的大小．
解答：取BC的中点G，连接EG，FG，如下图所示：
则EG平行且等于PB的一半，FG平行且等于AC的一半
即∠EGF即为直线PB与直线AC所成角
∵EF=5，PB=8，AC=6
∴EG=4，FG=3
∵EG2+FG2=EF2，
∴∠EGF=90°
故直线PB与直线AC所成角的大小为90°
故答案为：90°
点评：本题考查的知识点是异面直线及其所成的角，其中根据异面直线夹角的定义，利用“平移法”得到∠EGF即为直线PB与直线AC所成角，是解答本题的关键．
分析：取BC的中点G，连接EG，FG，由三角形的中位线定理，可得EG∥PB，FG∥AC，即∠EGF即为直线PB与直线AC所成角，根据EF=5，PB=8，AC=6，解三角形EFG，即可得到直线PB与直线AC所成角的大小．
解答：取BC的中点G，连接EG，FG，如下图所示：
则EG平行且等于PB的一半，FG平行且等于AC的一半
即∠EGF即为直线PB与直线AC所成角
∵EF=5，PB=8，AC=6
∴EG=4，FG=3
∵EG2+FG2=EF2，
∴∠EGF=90°
故直线PB与直线AC所成角的大小为90°
故答案为：90°
点评：本题考查的知识点是异面直线及其所成的角，其中根据异面直线夹角的定义，利用“平移法”得到∠EGF即为直线PB与直线AC所成角，是解答本题的关键．
练习册系列答案
相关题目
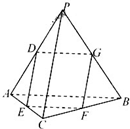如图，在四面体PABC中，PC⊥AB，PA⊥BC，点D，E，F，G分别是棱AP，AC，BC，PB的中点．
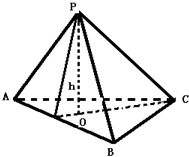在Rt△ABC中，CA⊥CB，斜边AB上的高为
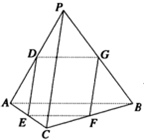如图，在四面体P-ABC中，PC⊥AB，PA⊥BC，点D、E、F、G分别是棱AP、AC、CB、BP的中点；
（2012•广州一模）如图，在四面体PABC中，PA=PB，CA=CB，D、E、F、G分别是PA、AC、CB、BP的中点．