题目内容
已知函数
(I)求函数f(x)的单调区间;
(Ⅱ)若对任意x1∈(0,2),总存在x2∈[1,2]使f(x1)≥g(x2),求实数m的取值范围.

(I)求函数f(x)的单调区间;
(Ⅱ)若对任意x1∈(0,2),总存在x2∈[1,2]使f(x1)≥g(x2),求实数m的取值范围.
解:(Ⅰ)函数的定义域为(0,+∞), =
=  ,
,
由f′(x)>0得,1<x<3,
由f′(x)<0得,0<x<1或x>3,
∴函数f(x)的单调递增区间为(1,3);
单调递减区间为(0,1),(3,+∞);
(Ⅱ) 由(Ⅰ)知函数f(x)在区间(0,1)上递减,在区间(1,2)上递增,
∴函数f(x)在区间(0,2)上的最小值为f(1)= ,
,
由于“对任意x1∈(0,2),总存在x2∈[1,2]使f(x1)≥g(x2)”
等价于“g(x)在区间[1,2]上的最小值不大于f(x)在区间(0,2)上的最小值 ”
”
即g(x)min≤ ,(*)
,(*)
又g(x)=x2﹣2mx+4,x∈[1,2],
∴①当m<1时,g(x)min=g(1)=5﹣2m>0与(*)式矛盾,
②当m∈[1,2]时,g(x)min=4﹣m2≥0,与(*)式矛盾,
③当m>2时,g(x)min=g(2)=8﹣4m≤ ,解得m
,解得m  ,
,
综上知,实数m的取值范围是[ ).
).
 =
=  ,
,由f′(x)>0得,1<x<3,
由f′(x)<0得,0<x<1或x>3,
∴函数f(x)的单调递增区间为(1,3);
单调递减区间为(0,1),(3,+∞);
(Ⅱ) 由(Ⅰ)知函数f(x)在区间(0,1)上递减,在区间(1,2)上递增,
∴函数f(x)在区间(0,2)上的最小值为f(1)=
 ,
,由于“对任意x1∈(0,2),总存在x2∈[1,2]使f(x1)≥g(x2)”
等价于“g(x)在区间[1,2]上的最小值不大于f(x)在区间(0,2)上的最小值
 ”
” 即g(x)min≤
 ,(*)
,(*)又g(x)=x2﹣2mx+4,x∈[1,2],
∴①当m<1时,g(x)min=g(1)=5﹣2m>0与(*)式矛盾,
②当m∈[1,2]时,g(x)min=4﹣m2≥0,与(*)式矛盾,
③当m>2时,g(x)min=g(2)=8﹣4m≤
 ,解得m
,解得m  ,
,综上知,实数m的取值范围是[
 ).
).
练习册系列答案
相关题目
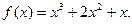
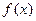 的单调区间与极值;
的单调区间与极值;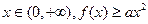 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。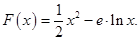
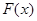 的最小值;
的最小值; 和
和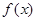 定义域内的任意实数
定义域内的任意实数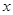 ,若存在常数
,若存在常数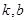 ,使得不等式
,使得不等式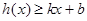 和
和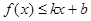 都成立,则称直线
都成立,则称直线 是函数
是函数 ,
,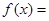
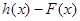 ,试问函数
,试问函数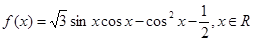
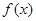 的最小值和最小正周期;
的最小值和最小正周期;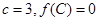 ,若向量
,若向量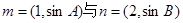 共线,求a,b的值。
共线,求a,b的值。