题目内容

方程2-x+x2=
2
实数解的个数为
2
2
．
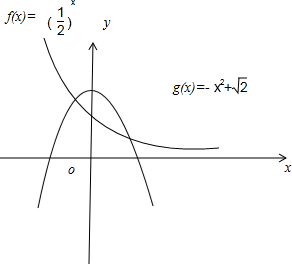
分析：构造函数f(x)=(
1
2
)x，g（x）=g(x)=-x2+
2
，要求方程2-x+x2=
2
有实数解的个数，只要求函数f（x）与函数g（x）的图象的交点个数即可
解答：解：令f(x)=(
1
2
)x，g（x）=g(x)=-x2+
2

结合图象可知函数f（x）与函数g（x）有两个交点
方程2-x+x2=
2
有2个实数解
故答案为：2
点评：本题主要考查了方程的解的个数的判断，转化为找函数的图象的交点的个数，体现了数形结合与转化思想在解题中的应用．
练习册系列答案
相关题目
2、方程2-x+x2=3的实数解的个数为（　　）
方程2-x+x2=3的实数解的个数为（　　）
若关于x的方程2-|x|-x2+a=0有两个不相等的实数解，则实数a的取值范围是
（-1，+∞）
（-1，+∞）
．
（2008•杨浦区二模）若曲线的参数方程为
x=|cos
θ
2
+sin
θ
2
y=
1
2
(1+sinθ)
(θ为参数，0≤θ≤π），则该曲线的普通方程为
x2=2y(1≤x≤
2
，
1
2
≤y≤1)
x2=2y(1≤x≤
2
，
1
2
≤y≤1)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网