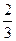题目内容
已知数列{an}的前n项和为Sn,且a1=1,nan+1=(n+2)Sn (n∈N*).
(1)求证:数列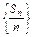 为等比数列;
为等比数列;
(2)求数列{an}的通项公式及前n项和Sn;
(3)若数列{bn}满足:b1=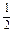 ,
,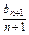 =
=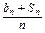 (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式.
(1)求证:数列
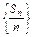 为等比数列;
为等比数列;(2)求数列{an}的通项公式及前n项和Sn;
(3)若数列{bn}满足:b1=
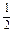 ,
,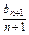 =
=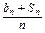 (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式.(1)证明见解析(2)an=(n+1)2n-2(n∈N*)(3) bn=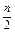 (2n-1) (n∈N*)
(2n-1) (n∈N*)
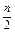 (2n-1) (n∈N*)
(2n-1) (n∈N*)(1)证明 将an+1=Sn+1-Sn代入已知nan+1=(n+2)Sn;
整理得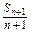 =2×
=2×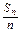 (n∈N*).
(n∈N*).
又由已知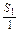 =1,
=1,
所以数列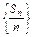 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.
(2)解 由(1)的结论可得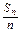 =2n-1,∴Sn=n·2n-1,
=2n-1,∴Sn=n·2n-1,
当n≥2时,
an=Sn-Sn-1=n·2n-1-(n-1)·2n-2=2n-2(n+1).
由已知,a1=1,又当n=1时,2n-2(n+1)=1,
∴an=(n+1)2n-2(n∈N*).
(3)解 由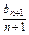 =
=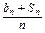 (n∈N*),得
(n∈N*),得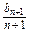 =
=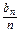 +2n-1,
+2n-1,
由此式可得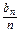 =
=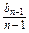 +2n-2,
+2n-2,
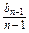 =
=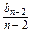 +2n-3,
+2n-3,
…
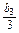 =
=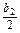 +23-2,
+23-2,
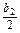 =
=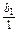 +22-2.
+22-2.
把以上各等式相加得,
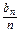 =2n-2+2n-3+…+23-2+22-2+b1.
=2n-2+2n-3+…+23-2+22-2+b1.
∵b1=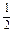 ,∴
,∴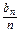 =
=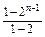 +
+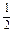 ,
,
∴bn=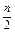 (2n-1) (n∈N*).
(2n-1) (n∈N*).
整理得
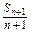 =2×
=2×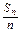 (n∈N*).
(n∈N*).又由已知
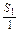 =1,
=1,所以数列
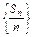 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.(2)解 由(1)的结论可得
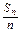 =2n-1,∴Sn=n·2n-1,
=2n-1,∴Sn=n·2n-1,当n≥2时,
an=Sn-Sn-1=n·2n-1-(n-1)·2n-2=2n-2(n+1).
由已知,a1=1,又当n=1时,2n-2(n+1)=1,
∴an=(n+1)2n-2(n∈N*).
(3)解 由
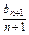 =
=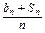 (n∈N*),得
(n∈N*),得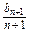 =
=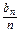 +2n-1,
+2n-1,由此式可得
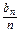 =
=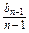 +2n-2,
+2n-2,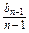 =
=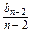 +2n-3,
+2n-3,…
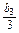 =
=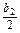 +23-2,
+23-2,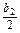 =
=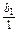 +22-2.
+22-2.把以上各等式相加得,
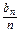 =2n-2+2n-3+…+23-2+22-2+b1.
=2n-2+2n-3+…+23-2+22-2+b1.∵b1=
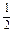 ,∴
,∴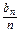 =
=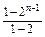 +
+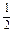 ,
,∴bn=
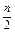 (2n-1) (n∈N*).
(2n-1) (n∈N*).
练习册系列答案
相关题目

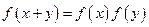
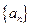 满足
满足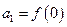 ,且
,且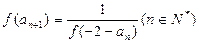 ,数列
,数列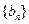 满足
满足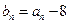
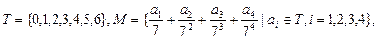 将M中的元素按从大到小的顺序排列,则第2005个数是( )
将M中的元素按从大到小的顺序排列,则第2005个数是( )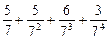
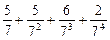
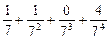
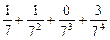
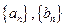
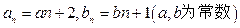
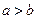
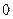 个
个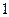 个
个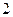 个
个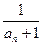 }为等差数列,则a11等于( )
}为等差数列,则a11等于( )