题目内容
已知点(a,b)在直线x+3y-2=0上,则u=3a+27b+3的最小值为( )
A、
| ||
B、3+2
| ||
| C、6 | ||
| D、9 |
分析:由于3a•27b=3a+3b是常数,利用基本不等式求3a+27b的最小值,从而得出u=3a+27b+3的最小值.
解答:解:∵2x+4y≥2
=2
又∵x+2y=2
∴3 a+27b+3≥2
+3=2
+3
=9
当且仅当3a=27b即a=3b时取等号
故选D
| 2x•4y |
| 2x+2y |
又∵x+2y=2
∴3 a+27b+3≥2
| 3 a• 3 3b |
| 3 a+3b |
=9
当且仅当3a=27b即a=3b时取等号
故选D
点评:本题考查利用基本不等式求函数的最值要注意满足:一正、二定、三相等.

练习册系列答案
相关题目
 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆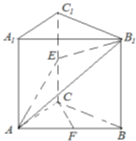 (2013•渭南二模)如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.
(2013•渭南二模)如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4. (本题满分12分)已知椭圆E:
(本题满分12分)已知椭圆E: