题目内容
计算下列各式:
(Ⅰ)(lg2)2+lg5lg20-1;
(Ⅱ) .
.
解:(Ⅰ)原式=lg22+(1-lg2)(1+lg2)-1(2分)
=lg22+1-lg22-1=0(3分)
(Ⅱ)原式= (1分)
(1分)
=-1+2×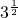 ×
× ×
× (2分)
(2分)
=-1+ ×
× =5.(2分)
=5.(2分)
分析:(Ⅰ)直接利用对数的性质,化简(lg2)2+lg5lg20-1,求出值即可.
(Ⅱ)利用指数幂的运算,无理式化分母为有理数,以及方式指数幂运算,求出结果即可.
点评:本题考查对数的运算性质,根式的化简运算,考查计算能力,是基础题.
=lg22+1-lg22-1=0(3分)
(Ⅱ)原式=
 (1分)
(1分)=-1+2×
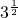 ×
× ×
× (2分)
(2分)=-1+
 ×
× =5.(2分)
=5.(2分)分析:(Ⅰ)直接利用对数的性质,化简(lg2)2+lg5lg20-1,求出值即可.
(Ⅱ)利用指数幂的运算,无理式化分母为有理数,以及方式指数幂运算,求出结果即可.
点评:本题考查对数的运算性质,根式的化简运算,考查计算能力,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目