题目内容
经市场调查,某超市的一种商品在过去的一个月内(以30天计),销售价格(元)与时间t(天)的函数关系近似满足f(t)=100(1+| 1 | t |
(1)试写出该商品的日销售金额w(t)关于时间t(1≤t≤30,t∈N)的函数表达式;
(2)求该商品的日销售金额w(t)的最大值与最小值.
分析:(1)函数关系近似满足f(t)=100(1+
),、g(t)=125-|t-25|,即可得到商品的日销售金额w(t)关于时间t(1≤t≤30,t∈N)的函数关系式;
(2)由函数关系近似满足f(t)=100(1+
),判断函数的单调性判断出函数的最值,即该商品的日销售金额w(t)的最值.
| 1 |
| t |
(2)由函数关系近似满足f(t)=100(1+
| 1 |
| t |
解答:解:(1)由题意,得
w(t)=f(t)•g(t)=100(1+
)(125-|t-25|)
=
(2)①当1≤t<25时,因为t+
≥20,
所以当t=10时,w(t)有最小值12100;
当t=1时,w(t)有最大值20200;
②当25≤t≤30时,∵
-t在[25,30]上递减,
∴当t=30时,w(t)有最小值12400
∵12100<12400,
∴当t=10时,
该商品的日销售金额w(t)取得最小值为12100.
最大值为20200.
w(t)=f(t)•g(t)=100(1+
| 1 |
| t |
=
|
|
(2)①当1≤t<25时,因为t+
| 100 |
| t |
所以当t=10时,w(t)有最小值12100;
当t=1时,w(t)有最大值20200;
②当25≤t≤30时,∵
| 150 |
| t |
∴当t=30时,w(t)有最小值12400
∵12100<12400,
∴当t=10时,
该商品的日销售金额w(t)取得最小值为12100.
最大值为20200.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-
的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-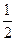 |t-10|.
|t-10|.  (元).
(元). |t-10|.
|t-10|.