题目内容
在数列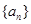 中,
中,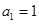 ,当
,当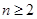 时,
时,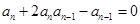
(Ⅰ)求数列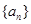 的通项公式;
的通项公式;
(Ⅱ)设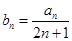 ,求数列
,求数列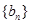 的前
的前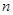 项和
项和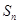 .
.
【解析】本试题主要考查了数列的通项公式的求和 综合运用。第一问中 ,利用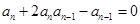 ,得到
,得到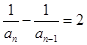 且
且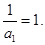 ,故故
,故故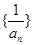 为以1为首项,公差为2的等差数列. 从而
为以1为首项,公差为2的等差数列. 从而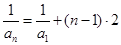

第二问中,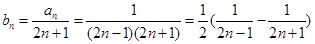
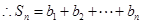
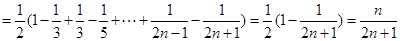
由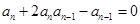 及
及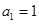 知
知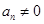 ,从而可得
,从而可得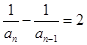 且
且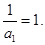
故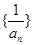 为以1为首项,公差为2的等差数列.
为以1为首项,公差为2的等差数列.
从而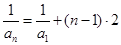
 ……………………6分
……………………6分
(2)
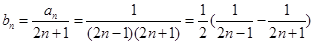 ……………………9分
……………………9分
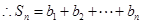
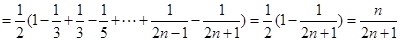
【答案】
 (2)
(2)


练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 具有如下性质:①
具有如下性质:①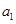 为正整数;②对于任意的正整数
为正整数;②对于任意的正整数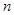 ,当
,当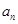 为偶数时,
为偶数时,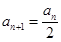 ;当
;当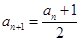 .在数列
.在数列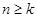 时,
时,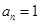 ,当
,当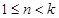 时,
时,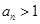 (
(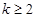 ,
,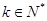 ),则首项
),则首项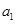 可取数值的个数为 (用
可取数值的个数为 (用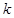 表示)
表示)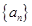 具有如下性质:①
具有如下性质:①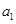 为正整数;②对于任意的正整数
为正整数;②对于任意的正整数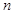 ,当
,当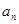 为偶数时,
为偶数时,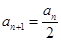 ;当
;当 .在数列
.在数列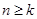 时,
时,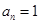 ,当
,当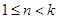 时,
时,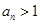 (
(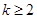 ,
, ),则首项
),则首项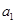 可取数值的个数为 (用
可取数值的个数为 (用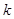 表示)
表示)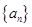 具有如下性质:①
具有如下性质:①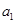 为正整数;②对于任意的正整数
为正整数;②对于任意的正整数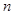 ,当
,当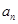 为偶数时,
为偶数时,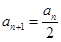 ;当
;当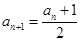 .在数列
.在数列 时,
时,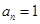 ,当
,当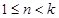 时,
时,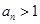 (
(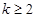 ,
,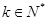 ),则首项
),则首项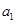 可取数值的个数为 (用
可取数值的个数为 (用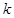 表示)
表示) 中,
中, ,当
,当 时,其前
时,其前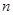 项和
项和 满足
满足 .
. ,求数列
,求数列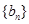 的前项和
的前项和 .
. ;
;