题目内容
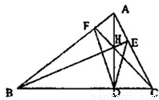
 如图,AD是△ABC边BC上的高.
如图,AD是△ABC边BC上的高.
(1)若△ABC的面积S= ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;
(2)若△ABC另外两条边上的高BE,CF 与AD相交于点H,求证:AD平分∠EDF.
解:(1)若△ABC的面积S= ,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2
,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2 .
.
(2)∵△ABC另外两条边上的高BE,CF 与AD相交于点H,∴∠HDB=∠HFB=90°,故BDHF四点共圆,
∴∠FBH=∠FDH.
同理可得,∠ECH=∠EDH.
又∠FBH=90°-A,∠ECH=90°-A,∴∠FDH=∠EDH,即 AD平分∠EDF.
分析:(1)若△ABC的面积S= ,则A=90°,由射影定理求得斜边上的高AD的值.
,则A=90°,由射影定理求得斜边上的高AD的值.
(2)先判断BDHF四点共圆,可得∠FBH=∠FDH.同理可得,∠ECH=∠EDH.再由∠FBH=90°-A,∠ECH=90°-A 可得∠FDH=∠EDH,从而得出结论.
点评:本题主要考查圆内接多边形的性质、解三角形,属于中档题.
 ,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2
,则A=90°,由射影定理可得 AD2=BD•CD=4×3=12,∴AD=2 .
.
(2)∵△ABC另外两条边上的高BE,CF 与AD相交于点H,∴∠HDB=∠HFB=90°,故BDHF四点共圆,
∴∠FBH=∠FDH.
同理可得,∠ECH=∠EDH.
又∠FBH=90°-A,∠ECH=90°-A,∴∠FDH=∠EDH,即 AD平分∠EDF.
分析:(1)若△ABC的面积S=
 ,则A=90°,由射影定理求得斜边上的高AD的值.
,则A=90°,由射影定理求得斜边上的高AD的值.(2)先判断BDHF四点共圆,可得∠FBH=∠FDH.同理可得,∠ECH=∠EDH.再由∠FBH=90°-A,∠ECH=90°-A 可得∠FDH=∠EDH,从而得出结论.
点评:本题主要考查圆内接多边形的性质、解三角形,属于中档题.

练习册系列答案
相关题目
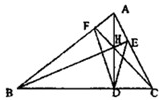 如图,AD是△ABC边BC上的高.
如图,AD是△ABC边BC上的高. (2012•江门一模)(几何证明选讲选做题)如图,AD是△ABC的高,AE是△ABC外接圆的直径.若AB=6,AC=5,AD=4,则图中与∠BAE相等的角是
(2012•江门一模)(几何证明选讲选做题)如图,AD是△ABC的高,AE是△ABC外接圆的直径.若AB=6,AC=5,AD=4,则图中与∠BAE相等的角是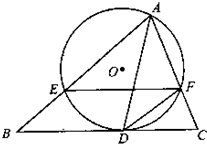 (2009•大连一模)选修4-1:几何证明选讲
(2009•大连一模)选修4-1:几何证明选讲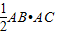 ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;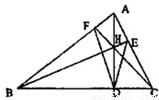
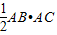 ,BD=4,DC=3,求AD的长;
,BD=4,DC=3,求AD的长;