题目内容
5. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F(1,0),且点(-1,$\frac{3}{2}$)在椭圆上,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F(1,0),且点(-1,$\frac{3}{2}$)在椭圆上,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.(Ⅰ)求椭圆C的方程;
(Ⅱ)求$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围;
(Ⅲ)若点B关于x轴的对称点是E,证明:直线AE过定点.
分析 (Ⅰ)可知c=1,从而得a2=b2+1,$\frac{1}{{a}^{2}}$+$\frac{\frac{9}{4}}{{b}^{2}}$=1,从而求得椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)由题意知直线AB的斜率存在,故设直线AB的方程为y=k(x-4);与椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1联立化简可得(4k2+3)x2-32k2x+64k2-12=0;从而可解得k2<$\frac{1}{4}$;再设A(x1,y1),B(x2,y2);从而可得x1+x2=$\frac{32{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{64{k}^{2}-12}{4{k}^{2}+3}$;化简y1y2=k(x1-4)k(x2-4)=k2x1x2-4k2(x1+x2)+16k2,从而可得$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+k2)$\frac{64{k}^{2}-12}{4{k}^{2}+3}$-4k2$\frac{32{k}^{2}}{4{k}^{2}+3}$+16k2=25-$\frac{87}{4{k}^{2}+3}$;从而求其取值范围;
(Ⅲ)可设E(x2,-y2);从而写出直线AE的方程为y-y1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),令y=0并化简可得x=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$;再将x1+x2=$\frac{32{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{64{k}^{2}-12}{4{k}^{2}+3}$代入化简可得x=1;从而证明.
解答 解:(Ⅰ)由题意,c=1,
a2=b2+1,$\frac{1}{{a}^{2}}$+$\frac{\frac{9}{4}}{{b}^{2}}$=1,
解得,a2=4,b2=3;
故椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)由题意知直线AB的斜率存在,
设直线AB的方程为y=k(x-4);
与椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1联立化简可得,
(4k2+3)x2-32k2x+64k2-12=0;
则令△=(-32k2)2-4(4k2+3)(64k2-12)>0得,
k2<$\frac{1}{4}$;
设A(x1,y1),B(x2,y2);
则x1+x2=$\frac{32{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{64{k}^{2}-12}{4{k}^{2}+3}$;
则y1y2=k(x1-4)k(x2-4)=k2x1x2-4k2(x1+x2)+16k2,
则$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+k2)$\frac{64{k}^{2}-12}{4{k}^{2}+3}$-4k2$\frac{32{k}^{2}}{4{k}^{2}+3}$+16k2=25-$\frac{87}{4{k}^{2}+3}$;
∵0≤k2<$\frac{1}{4}$,
∴-$\frac{87}{3}$≤-$\frac{87}{4{k}^{2}+3}$<-$\frac{87}{4}$;
∴$\overrightarrow{OA}•\overrightarrow{OB}$∈[-4,$\frac{13}{4}$).
(Ⅲ)证明:∵点B关于x轴的对称点是E,
∴E(x2,-y2);
直线AE的方程为
y-y1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),
令y=0得,
x=x1-$\frac{{y}_{1}({x}_{1}-{x}_{2})}{{y}_{1}+{y}_{2}}$
=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$;
将x1+x2=$\frac{32{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{64{k}^{2}-12}{4{k}^{2}+3}$代入化简可得,
x=1;
故直线AE与x轴交于定点(1,0).
即直线AE过定点.
点评 本题考查了椭圆的方程的求法及学生的化简与运算能力,化简很复杂,属于难题.

| A. | -$\frac{2}{3}π$ | B. | $\frac{2}{3}π$ | C. | -$\frac{5}{6}π$ | D. | $\frac{5}{6}π$ |
 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的图象与
的图象与 轴围成的三角形面积大于6,求
轴围成的三角形面积大于6,求 的取值范围.
的取值范围. ,下列命题正确的是 .
,下列命题正确的是 . 关于原点
关于原点 中心对称;
中心对称; ,
, 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与 交于
交于 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系 ;
; 为切点,作切线与
为切点,作切线与 ,再以点
,再以点 为切点作直线与
为切点作直线与 ,再以点
,再以点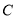 作切点作直线与
作切点作直线与 ,则
,则 点横坐标为
点横坐标为 ;
;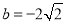 ,函数
,函数 ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形. 万件与每台机器的日产量
万件与每台机器的日产量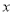 万件
万件 之间满足关系:
之间满足关系: .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元. 表示为
表示为 的函数;
的函数; 与
与 都是I的子集(如图所示),则阴影部分所表示的集合为( )
都是I的子集(如图所示),则阴影部分所表示的集合为( )
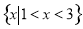 B.
B.
 D.
D.