题目内容
曲线 在x=0点处的切线方程是
在x=0点处的切线方程是
- A.x+yln2-ln2=0
- B.xln2+y-1=0
- C.x-y+1=0
- D.x+y-1=0
B
分析:求导函数,求得切线的斜率,再求出切点的坐标,即可得到结论.
解答:求导数可得 ,当x=0时,y′=-ln2
,当x=0时,y′=-ln2
∵x=0时,
∴曲线 在x=0点处的切线方程是y-1=-xln2,即xln2+y-1=0
在x=0点处的切线方程是y-1=-xln2,即xln2+y-1=0
故选B.
点评:本题考查导数的几何意义,考查切线方程,属于基础题.
分析:求导函数,求得切线的斜率,再求出切点的坐标,即可得到结论.
解答:求导数可得
 ,当x=0时,y′=-ln2
,当x=0时,y′=-ln2∵x=0时,

∴曲线
 在x=0点处的切线方程是y-1=-xln2,即xln2+y-1=0
在x=0点处的切线方程是y-1=-xln2,即xln2+y-1=0故选B.
点评:本题考查导数的几何意义,考查切线方程,属于基础题.

练习册系列答案
相关题目
 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y= =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=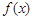 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=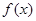 ≤2x-2.
≤2x-2. =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=