题目内容
已知函数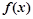 对任意实数
对任意实数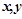 恒有
恒有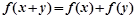 且当x>0,
且当x>0,
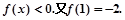
(1)判断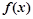 的奇偶性;
的奇偶性;
(2)求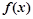 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)解关于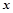 的不等式
的不等式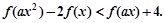
【答案】
(1) 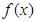 为奇函数(2)
6 (3)见解析
为奇函数(2)
6 (3)见解析
【解析】本试题主要考查了函数的奇偶性和单调性以及不等式的求解综合运用。
(1)运用赋值法思想得到函数的 奇偶性的判定。
(2)先证明函数的单调性,然后利用单调性证明不等式。
(3)对于参数a分情况讨论得到解集。
解(1)取 则
则 ………………1′
………………1′
取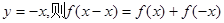
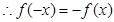 对任意
对任意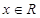 恒成立 ∴
恒成立 ∴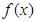 为奇函数. ………………3′
为奇函数. ………………3′
(2)任取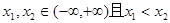 ,
则
,
则
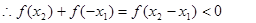 ………………4′
………………4′
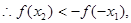 又
又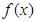 为奇函数
为奇函数 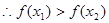
∴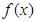 在(-∞,+∞)上是减函数.
在(-∞,+∞)上是减函数.
 对任意
对任意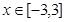 ,恒有
,恒有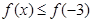 ………………6′
………………6′
而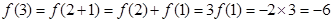
 ∴
∴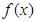 在[-3,3]上的最大值为6………………8′
在[-3,3]上的最大值为6………………8′
(3)∵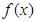 为奇函数,∴整理原式得
为奇函数,∴整理原式得
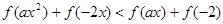
进一步可得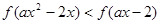
而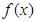 在(-∞,+∞)上是减函数,
在(-∞,+∞)上是减函数, ………………10′
………………10′

 当
当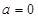 时,
时,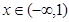
当 时,
时,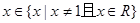
当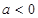 时,
时,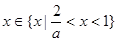

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
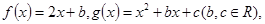 对任意的
对任意的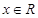 恒有
恒有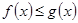 成立.
成立.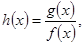 若
若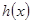 在
在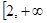 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;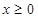 时,
时,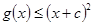 成立;
成立;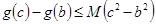 恒成立,求M的最小值.
恒成立,求M的最小值.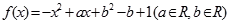 ,对任意实数
,对任意实数 都有
都有 成立,若当
成立,若当 时,
时, 恒成立,则
恒成立,则 的取值范围是
的取值范围是 B.
B. 或
或  C.
C.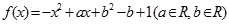 ,对任意实数
,对任意实数 都有
都有 成立,若当
成立,若当 时,
时, 恒成立,则
恒成立,则 的取值范围是
的取值范围是 B.
B. 或
或 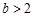 C.
C.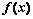 对任意实数
对任意实数 恒有
恒有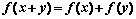 且当x>0,
且当x>0,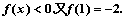
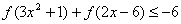 .
.