题目内容
已知函数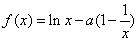 ,
,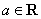 .
.
(1)求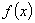 的单调区间;
的单调区间;
(2)若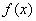 的最小值为0,回答下列问题:
的最小值为0,回答下列问题:
(ⅰ)求实数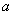 的值;
的值;
|
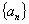 满足
满足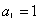 ,
,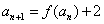 ,记[
,记[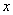 ]表示不大于
]表示不大于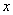 的最大整数,求
的最大整数,求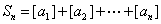 ,求
,求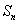 .
.
解:(1)函数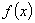 的定义域为
的定义域为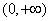 ,且
,且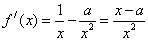 .
.
当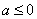 时,
时,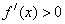 ,所以
,所以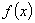 在区间
在区间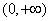 内单调递增;
内单调递增;
当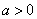 时,由
时,由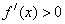 ,解得
,解得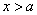 ;由
;由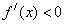 ,解得
,解得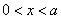 .
.
所以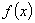 的单调递增区间为
的单调递增区间为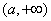 ,单调递减区间为
,单调递减区间为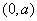 .
.
综上述: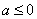 时,
时,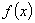 的单调递增区间是
的单调递增区间是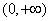 ;
;
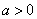 时,
时,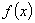 的单调递减区间是
的单调递减区间是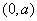 ,单调递增区间是
,单调递增区间是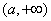 .
.
(2)(ⅰ)由(1)知,当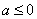 时,
时,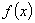 无最小值,不合题意;
无最小值,不合题意;
当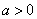 时,
时,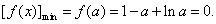
令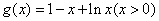 ,则
,则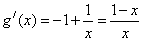 ,
,
由 ,解得
,解得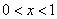 ;由
;由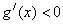 ,解得
,解得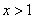 .
.
所以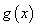 的单调递增区间为
的单调递增区间为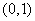 ,单调递减区间为
,单调递减区间为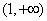 .
.
故 ,即当且仅当x=1时,
,即当且仅当x=1时,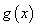 =0.
=0.
因此, .
.
(ⅱ)因为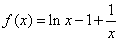 ,所以
,所以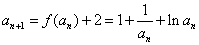 .
.
由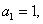 得
得 于是
于是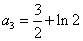 .因为
.因为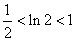 ,所以
,所以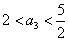 .
.
猜想当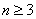 ,
, 时,
时, .
.
下面用数学归纳法进行证明.
①当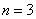 时,
时,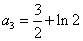 ,故
,故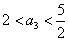 成立.
成立.
②假设当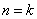 (
(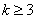 ,
,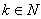 )时,不等式
)时,不等式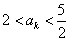 成立. 则当
成立. 则当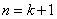 时,
时,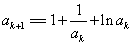 ,
,
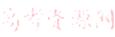 由(1)知函数
由(1)知函数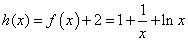 在区间
在区间 单调递增,
单调递增,
所以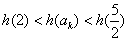 ,又因为
,又因为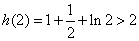 ,
,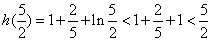 .
.
故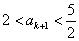 成立,即当
成立,即当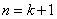 时,不等式成立.
时,不等式成立.
根据①②可知,当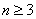 ,
, 时,不等式
时,不等式 成立.
成立.
|

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ,
,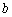 ,
,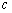 都在函数
都在函数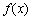 的定义域内,就有
的定义域内,就有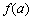 ,
,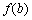 ,
,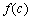 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称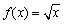 ; ②
; ②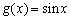
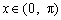 ; ③
; ③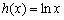
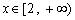 ,
,


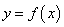 在区间
在区间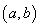 上的导函数为
上的导函数为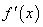 ,
,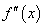 ,若在区间
,若在区间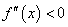 恒成立,则称函数
恒成立,则称函数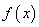 在区间
在区间 ,若对任意满足
,若对任意满足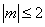 的实数
的实数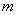 ,函数
,函数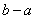 的最大值为
的最大值为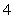 B.
B. C.
C.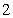 D.
D.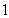
 中,
中, 是边
是边 的中点,且
的中点,且 ,
, .
. 的值;
的值; 的值.
的值. 变为曲线
变为曲线 的伸缩变换是( )
的伸缩变换是( ) B.
B.  C.
C. D.
D.
 ,则f(2012)的值为( )
,则f(2012)的值为( )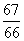 升 C.
升 C.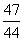 升 D.
升 D.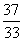 升
升