题目内容
(1)已知f(x)=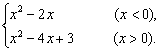 求f{f[f(-4)]};?
求f{f[f(-4)]};? (2)已知f(x)=x2-1,?g(x)=![]() 求f(g(x))与g(f(x)).?
求f(g(x))与g(f(x)).?
解:(1)∵-4<0,?∴f(-4)=(-4)+4=0.?
∴f(f(-4))=f(0)=1.于是f{f[f(-4)]}=f(f(0))=f(1)=12+3=4.?
(2)当x>0时,g(x)=2-x,f(g(x))=(2-x)2-1=x2-4x+3.?
当x<0时,g(x)=x-1,f(g(x))=(x-1)2-1=x2-2x,故f(g(x))=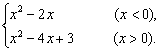
当x2-1<0,即-1<x<1时,f(x)<0,所以g(f(x))=f(x)-1=x2-2.?
当x2-1>0,即x>1或x<-1时,f(x)<0,
所以g(f(x))=2-f(x)=3-x2.?
故g(f(x))=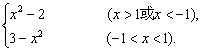
点评:本题涉及分段函数和复合函数的综合问题,注意分析自变量取不同值时,对函数解析式的选取.一般地,分段函数的复合函数仍然是分段函数.

练习册系列答案
相关题目
 的反函数.
的反函数. ax2+3x+5(a>0).
ax2+3x+5(a>0). )=
)= +1,求f (x) 的解析式. (不必写出定义域)
+1,求f (x) 的解析式. (不必写出定义域)