题目内容
直线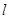 过椭圆
过椭圆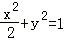 的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .
的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .
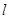 过椭圆
过椭圆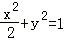 的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .
的左焦点F,且与椭圆相交于P、Q两点,M为PQ的中点,O为原点.若△FMO是以OF为底边的等腰三角形,则直线l的方程为 .
试题分析:由条件有
 ,则
,则 ,
,设
 ,
, ,则
,则 ,
,由条件
 ,作
,作 于
于 ,则
,则 为
为 中点,
中点,∴
 ,即
,即 ,
,设直线
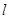 斜率为
斜率为 ,则直线
,则直线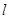 的方程为
的方程为 ,
,∴
 ,消
,消 得:
得: ,
,∴
 ,即
,即 ,即
,即 ,
,∴直线
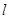 的方程为
的方程为 .
.
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 的两个焦点坐标是
的两个焦点坐标是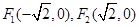 ,且离心率为
,且离心率为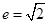 ;
; 表示曲线
表示曲线 轴左边部分,若直线
轴左边部分,若直线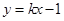 与曲线
与曲线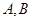 两点,求
两点,求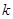 的取值范围;
的取值范围;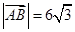 ,且曲线
,且曲线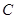 ,使
,使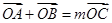 ,求
,求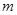 的值.
的值.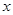 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为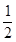
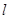 经过点
经过点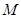 (0,1),且与椭圆交于
(0,1),且与椭圆交于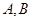 两点,若
两点,若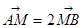 ,求直线
,求直线 中,已知椭圆
中,已知椭圆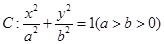 经过点
经过点
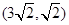 ,椭圆的离心率
,椭圆的离心率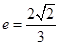 .
.
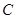 的方程;
的方程;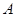 、
、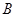 .若
.若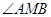 的平分线与
的平分线与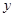 轴平行, 试探究直线
轴平行, 试探究直线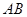 的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由.
的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由.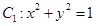 在矩阵
在矩阵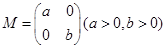 的变换作用下得到曲线
的变换作用下得到曲线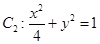 .
.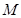 ;
;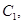 抛物线
抛物线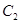 的焦点均在
的焦点均在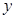 轴上,
轴上,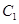 的中心和
的中心和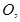 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中: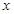
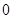
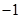
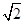
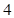
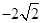
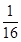
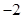
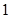
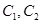 的方程的点的坐标;
的方程的点的坐标;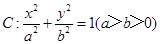 的离心率为
的离心率为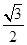 ,过右焦点
,过右焦点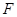 且斜率为
且斜率为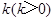 的直线与
的直线与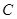 相交于
相交于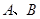 两点.若
两点.若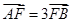 ,则
,则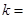 ( )
( )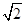
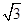
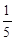
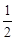
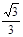
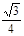

 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为直径的圆与双曲线渐近线的一个交点为
为直径的圆与双曲线渐近线的一个交点为 ,则此双曲线的方程为( )
,则此双曲线的方程为( )


