题目内容
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
C
解析试题分析:

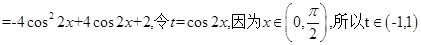 ,所以
,所以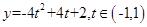 ,所以
,所以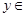
 。
。
考点: 和差公式;二倍角公式;二次函数在某闭区间上的最值。
点评:此题的关键是对函数进行化简,我们可以利用凑角的方法,利用和差公式从而达到异角化同角的目的。这一步的化简有点难度,我们在平常的学习中要注意掌握。

练习册系列答案
相关题目
函数 ( )
( )
A. | B. | C. | D. |
已知 ,且
,且 为奇函数,若
为奇函数,若 ,则
,则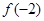 的值为
的值为
A. | B. | C. | D. |
函数 的定义域是 ( )
的定义域是 ( )
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
函数 的零点所在的大致区间是
的零点所在的大致区间是
| A.(6,7) | B.(7,8) | C.(8,9) | D.(9,10) |
函数 的图象如右图所示,下列说法正确的是( )
的图象如右图所示,下列说法正确的是( )
①函数 满足
满足
②函数 满足
满足
③函数 满足
满足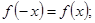
④函数 满足
满足

| A.①③ | B.②④ | C.①② | D.③④ |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D.1 |