题目内容
如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,D点的坐标为(2,1),求p的值.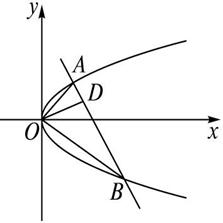
解:设A(x1,y1),B(x2,y2).
由OA⊥OB,得x1x2+y1y2=0.
由已知,直线AB的方程为y=-2x+5,则有y1y2-(y1+y2)+5=0. ①
由y=-2x+5与y2=2px消去x,得
y2+py-5p=0. ②
y1+y2=-p,y1y2=-5p. ③
把③代入①,解得p=![]() .
.
当p=![]() 时,方程②成为4y2+5y-25=0.
时,方程②成为4y2+5y-25=0.
显然此方程有实根.
所以p=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆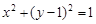 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求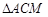 与
与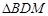 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
