题目内容
（本题满分14分）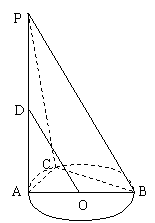
如图，AB是圆O的直径，PA垂直于圆O所在平面，C是圆上不同于A、B的任一点，D为PA中点．
求证：(1) OD∥平面PBC； (2) BC⊥平面PAC．
解：(1)∵O、D为AB、PA的中点
∴OD∥PB …………………………3分
又因为OD
平面PBC，PB
平面PBC …………………………5分
所以OD∥平面PBC …………………………7分
(2) ∵PA⊥平面ABC，BC平面ABC
∴PA⊥BC
∵AB是圆O的直径
∴AC⊥BC …………………………11分
又因为AC、PA平面PAC， AC∩PA =A …………………………12分
所以BC⊥平面PAC …………………………14分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；