题目内容
19.已知圆的一般方程x2+y2-4x-2y-5=0,其半径是$\sqrt{10}$.分析 将一般方程化为标准方程得出半径.
解答 解:圆的标准方程为(x-2)2+(y-1)2=10.
∴圆的半径为$\sqrt{10}$.
故答案为$\sqrt{10}$.
点评 本题考查了圆的一般方程,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
9.已知2a=3b=k(k≠1),且2a+b=2ab,则实数k的值为( )
| A. | 18 | B. | 18 或-18 | C. | $3\sqrt{2}$或 $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
7.用反证法证明命题“设a,b为实数,则方程x3+ax2+b=0至少有一个实根”时,要做的假设是( )
| A. | 方程x3+ax2+b=0至多有一个实根 | B. | 方程x3+ax2+b=0没有实根 | ||
| C. | 方程x3+ax2+b=0至多有两个实根 | D. | 方程x3+ax2+b=0恰好有两个实根 |
11.将函数f(x)=2sin(2x-$\frac{π}{4}$)的图象向左平移$\frac{π}{4}$个单位,得到函数g(x)的图象,则g(0)=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | -$\sqrt{2}$ |
9.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足f'(x1)=$\frac{f(b)-f(a)}{b-a}$,f'(x2)=$\frac{f(b)-f(a)}{b-a}$,则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)=2x3-x2+m是[0,2a]上“双中值函数”,则实数a的取值范围是( )
| A. | ($\frac{1}{8}$,$\frac{1}{4}$) | B. | ($\frac{1}{12}$,$\frac{1}{4}$) | C. | ($\frac{1}{12}$,$\frac{1}{8}$) | D. | ($\frac{1}{8}$,1) |
 已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.
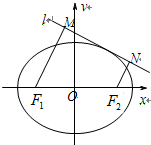
已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切. 如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.
如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.