已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}.x≤1}\\{lo{g} {3}(x-1).x＞1}\end{array}\right.$.且f(x0)=1.则x0=( )A．0B．4C．0或4D．1或3 题目和参考答案——青夏教育精英家教网—

题目内容

19．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤1}\\{lo{g}_{3}（x-1），x＞1}\end{array}\right.$，且f（x₀）=1，则x₀=（　　）

A．

B．

C．

0或4

D．

1或3

分析由f（x₀）=1，得到x₀的两个方程解之即可．

解答解：当x≤1时，由$f（{x_0}）={2^{x_0}}=1$得x₀=0；
当x＞1时，由f（x₀）=log₃（x₀-1）=1得x₀-1=3，
则x₀=4，且两者都成立；
故选：C．

点评本题考查了已知分段函数的函数值求自变量；考查了讨论的思想；注意分段函数的一个函数值可能对应多个自变量．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

10．命题“?x₀∈R，2${\;}^{{x}_{0}}$≥1”的否定是（　　）

A．

?x₀∈R，2${\;}^{{x}_{0}}$＜1

B．

?x₀∈R，2${\;}^{{x}_{0}}$≤1

7．化简：$\frac{cos（π+α）ta{n}^{2}（2π-α）cos（α-3π）}{sin（π-α）sin（2π-α）}$．

14．已知{a_n}为等差数列，且满足a₁+a₃=8，a₂+a₄=12．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）记{a_n}的前n项和为S_n，若a₃，a_k+1，S_k成等比数列，求正整数k的值．

4．在投掷一枚硬币的试验中，共投掷了100次，“正面朝上”的频数49，则“正面朝上”的频率为（　　）

11．某校高一年段为了控制学生迟到现象，特别规定在每周周一到周五这五天中，“连续5天，每天迟到都不超过5人次的班级才有资格争夺年段流动红旗”．根据过去5天年段统计的一到四班迟到学生人此数据的数字特征，一定有资格的是（　　）

	A．	一班：总体均值为2，总体方差为2		B．	二班：总体均值为3，中位数为3
	C．	三班：总体均值为2，总体方差大于0		D．	四班：中位数为2，众数为2

8．

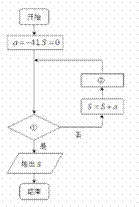右图表示的是求首项为-41，公差为2的等差数列{a_n}前n项和的最小值的程序框图．①处可填写a＞0；②处可填写a=a+2．

9．已知数列{a_n}为等差数列，其公差为-2，且a₅是a₂与a₇的等比中项，S_n为{a_n}（n∈N^*）的前n项和，则S₈的值为（　　）

试题分类