题目内容
设函数f（x）=（a-2）ln（-x）+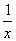
+2ax（a∈R），
（Ⅰ）当a=0时，求f（x）的极值；
（Ⅱ）当a≠0时，求f（x）的单调区间。
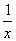+2ax（a∈R），（Ⅰ）当a=0时，求f（x）的极值；
（Ⅱ）当a≠0时，求f（x）的单调区间。
解：（Ⅰ）依题意，知f（x）的定义域为（-∞，0），
当a=0时，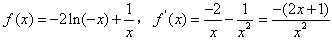
，
令f′（x）=0，解得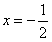
，
当x变化时，f′（x）与f（x）的变化情况如下表：
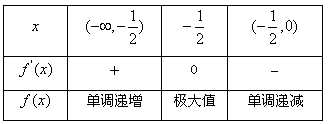
由上表知：当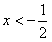
时，f′（x）＞0；当
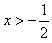时，f′（x）＜0，
故当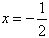
时，f（x）取得极大值为2ln2-2；
（Ⅱ）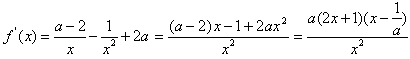
，
若a＞0，令f′（x）＞0，解得：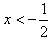
；令f′（x）＜0，解得：
；
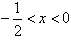若a＜0，
①当-2＜a＜0时，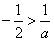
，
令f′（x）＞0，解得：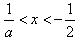
；
令f′（x）＜0，解得：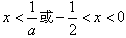
；
②当a=-2时，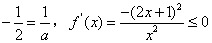
；
③当a＜-2时，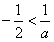
，
令f′（x）＞0，解得：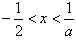
；
令f′（x）＜0，解得：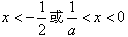
；
综上，当a＞0时，f（x）的增区间为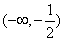
，减区间为
；
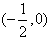当-2＜a＜0时，f（x）的增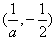区间为
，减区间为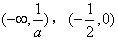
；
当a=-2时，f（x）的减区间为（-∞，0），无增区间；
当a＜-2时，f（x）的增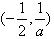区间为
，减区间为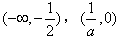
。
当a=0时，
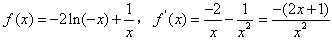，令f′（x）=0，解得
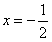，当x变化时，f′（x）与f（x）的变化情况如下表：
由上表知：当
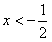时，f′（x）＞0；当
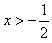时，f′（x）＜0，故当
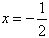时，f（x）取得极大值为2ln2-2；（Ⅱ）
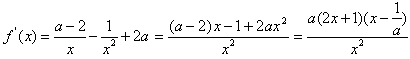，若a＞0，令f′（x）＞0，解得：
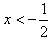；令f′（x）＜0，解得：
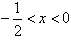；若a＜0，
①当-2＜a＜0时，
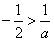，令f′（x）＞0，解得：
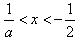；令f′（x）＜0，解得：
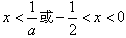；②当a=-2时，
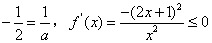；③当a＜-2时，
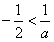，令f′（x）＞0，解得：
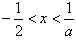；令f′（x）＜0，解得：
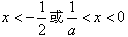；综上，当a＞0时，f（x）的增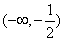区间为
，减区间为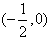
；当-2＜a＜0时，f（x）的增区间为
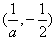，减区间为
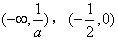；当a=-2时，f（x）的减区间为（-∞，0），无增区间；
当a＜-2时，f（x）的增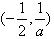区间为
，减区间为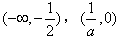
。
练习册系列答案
阅读快车系列答案
相关题目