Question

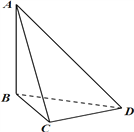
【题目】如图，在边长为4的菱形中，，现沿对角线把折起，折起后使的余弦值为

（1）求证：平面平面；

（2）若是的中点，求三棱锥的体积

Answer 1

【答案】(1)详见解析;(2) .

【解析】试题分析:(1) 菱形翻折后变成三棱锥，在中，由余弦定理求出,由勾股定理判断出，又，，由线面垂直的判定定理可得⊥平面,再由面面垂直的判定定理证明命题成立;(2) 因为是的中点，所以到平面的距离相等，由等体积法计算出三棱锥的体积.

试题解析:

（Ⅰ）证明：在菱形中，记的交点为，，∴，，翻折后变成三棱锥，在中，，

所以在中，，所以，

又，，∴⊥平面，又平面，

∴平面⊥平面．

（Ⅱ）解：因为是的中点，所以到平面的距离相等，

．

点睛:本题考查线面垂直的判定定理和面面垂直的判定定理以及锥体的体积公式. 判定直线和平面垂直的方法:①定义法．②利用判定定理：一条直线和一个平面内的两条相交直线都垂直，则该直线和此平面垂直．③推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条直线也垂直于这个平面．