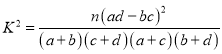题目内容
【题目】已知函数![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的值域;
的值域;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)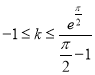 ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)先对函数求导,判断出函数单调性,进而可得出值域;
(2)先由题意,将问题转化为![]() 对任意
对任意![]() 恒成立,构造函数
恒成立,构造函数![]() ,对函数
,对函数![]() 求导,用导数方法判断其单调性,求其最小值,即可得出结果.
求导,用导数方法判断其单调性,求其最小值,即可得出结果.
(3)令![]() ,对函数
,对函数![]() 求导,用导数方法研究其单调性,求其最小值,只需最小值大于0即可.
求导,用导数方法研究其单调性,求其最小值,只需最小值大于0即可.
(1)因为![]() ,
,
所以![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,所以
,所以![]() ,
,
故函数![]() 在
在![]() 上单调递减,函数
上单调递减,函数![]() 的最大值为
的最大值为![]() ;
;
![]() 的最小值为
的最小值为![]() ,
,
所以函数![]() 的值域为
的值域为![]() .
.
(2)原不等式可化为![]() …(*),
…(*),
因为![]() 恒成立,故(*)式可化为
恒成立,故(*)式可化为![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,所以
,所以![]() ;
;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以当![]() ,即
,即![]() 时,函数
时,函数![]() 成立;
成立;
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,解得
,解得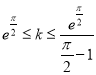
综上,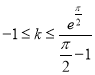 .
.
(3)令![]() ,则
,则![]() .
.
由![]() ,故存在
,故存在![]() ,使得
,使得![]() ,
,
即 ![]() .
.
所以,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故当![]() 时,函数
时,函数![]() 有极小值,且是唯一的极小值,
有极小值,且是唯一的极小值,
故函数![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故![]() ,
,
即![]() .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】携号转网,也称作号码携带、移机不改号,即无需改变自己的手机号码,就能转换运营商,并享受其提供的各种服务.2019年11月27日,工信部宣布携号转网在全国范围正式启动.某运营商为提质量保客户,从运营系统中选出300名客户,对业务水平和服务水平的评价进行统计,其中业务水平的满意率为![]() ,服务水平的满意率为
,服务水平的满意率为![]() ,对业务水平和服务水平都满意的客户有180人.
,对业务水平和服务水平都满意的客户有180人.
(Ⅰ)完成下面![]() 列联表,并分析是否有
列联表,并分析是否有![]() 的把握认为业务水平与服务水平有关;
的把握认为业务水平与服务水平有关;
对服务水平满意人数 | 对服务水平不满意人数 | 合计 | |
对业务水平满意人数 | |||
对业务水平不满意人数 | |||
合计 |
(Ⅱ)为进一步提高服务质量,在选出的对服务水平不满意的客户中,抽取2名征求改进意见,用![]() 表示对业务水平不满意的人数,求
表示对业务水平不满意的人数,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)若用频率代替概率,假定在业务服务协议终止时,对业务水平和服务水平两项都满意的客户流失率为![]() ,只对其中一项不满意的客户流失率为
,只对其中一项不满意的客户流失率为![]() ,对两项都不满意的客户流失率为
,对两项都不满意的客户流失率为![]() ,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
附: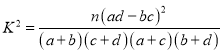 ,
,![]() .
.
0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |