题目内容
AB是⊙O的直径，弦CD⊥AB，垂足为M，AM=4，BM=9，则弦CD的长为
12
12
．分析：由已知中AB是⊙O的直径，弦CD⊥AB，垂足为M，根据垂径定理，我们可得M为CD的中点，结合已知中AM=4，BM=9，结合相交弦定理，我们可以求出CM及DM的长，进而求出弦CD的长．
解答：
解：已知如下图所示：
∵弦CD⊥AB，垂足为M，
∴CM=DM
由相交弦定理可得：
AM•BM=CM•DM
又∵AM=4，BM=9，
∴CM=DM=6
∴CD=12
故答案为：12
解：已知如下图所示：∵弦CD⊥AB，垂足为M，
∴CM=DM
由相交弦定理可得：
AM•BM=CM•DM
又∵AM=4，BM=9，
∴CM=DM=6
∴CD=12
故答案为：12
点评：本题考查的知识点是与圆有关的比例线段，垂径定理，其中根据垂径定理得到CM=DM，是解答本题的关键．
练习册系列答案
相关题目
如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F．求证：
选修4-1：几何证明选讲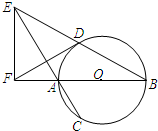
如图，AB是⊙O的直径，弦BD与CA延长线交于E点，EF⊥BA延长线于F，若∠AED=30°
（2012•郑州二模）选修4-1：平面几何