题目内容
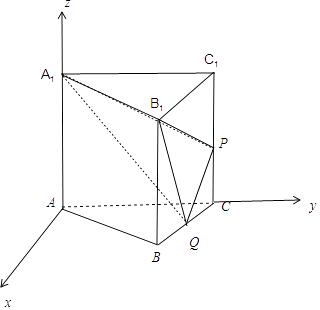
【题目】已知直三棱柱ABC﹣A1B1C1的所有棱长都为2,点P,Q分别为棱CC1 , BC的中点,则四面体A1﹣B1PQ的体积为 .
【答案】![]()
【解析】解:以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴, 建立空间直角坐标系,
A1(0,0,2),B1( ![]() ,1,2),
,1,2),
Q( ![]() ,
, ![]() ,0),P(0,2,1),
,0),P(0,2,1),![]() =(
=( ![]() ,﹣1,1),
,﹣1,1),![]() =(
=( ![]() ,﹣
,﹣ ![]() ,﹣1),
,﹣1), ![]() =(0,﹣2,1),
=(0,﹣2,1),
设平面PQB1的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,
,
取x=1,得 ![]() =(1,
=(1, ![]() ,0),
,0),
∴A1平面PQB1的距离d= ![]() =
= ![]() =
= ![]() ,
,
| ![]() |=
|= ![]() =
= ![]() ,|
,| ![]() |=
|= ![]() =
= ![]() ,
,
cos< ![]() >=
>= 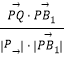 =
= ![]() =
= ![]() ,
,
sin< ![]() >=
>= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴四面体A1﹣B1PQ的体积为:
V= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙两组各有三名同学,他们在一次测试中的成绩分别为:甲组:88、89、90;乙组:87、88、92.如果分别从甲、乙两组中随机选取一名同学,则这两名同学的成绩之差的绝对值不超过3的概率是 .
【题目】2018年俄罗斯世界杯激战正酣,某校工会对全校教职工在世界杯期间每天收看比赛的时间作了一次调查,得到如下频数分布表:
收看时间 (单位:小时) |
|
|
|
|
|
|
| 14 |
|
| 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“球迷”,否则定义为“非球迷”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
球迷 | 40 | ||
非球迷 |
| ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“球迷”与“性别”有关;
(2)在全校“球迷”中按性别分层抽样抽取6名,再从这6名“球迷”中选取2名世界杯知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
![]() .
.
