题目内容
过椭圆右焦点F且倾斜角为45°的直线交椭圆于A、B两点，若|FB|=2|FA|，则椭圆的离心率为
．
| ||
| 3 |
| ||
| 3 |
分析：设椭圆的右准线为l，设A、B两点在l上的射影分别为C、D，连接AC、BD，过点B作BG⊥AC利用圆锥曲线的统一定义，再结合直角△ABG中，∠BAG=45°，可求出边之间的长度之比，可得离心率的值．
解答：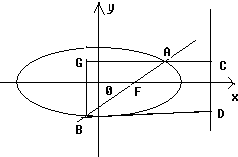
解：如图，设椭圆的右准线为l，过A点作AC⊥l于C，过点B作BD⊥l于D，再过B点作BG⊥AC于G，
在直角△ABG中，∠BAG=45°，所以AB=
AG，…①
由圆锥曲线统一定义得：e=
=
，
∵|FB|=2|AF|，∴|BD|=2|AC|，
在直角梯形ABDC中，AG=BD-AC=AC，…②
由①、②可得AB=
AC，
又∵AF=
AB=
AC，
∴e=
=
，
故答案为：
．
解：如图，设椭圆的右准线为l，过A点作AC⊥l于C，过点B作BD⊥l于D，再过B点作BG⊥AC于G，在直角△ABG中，∠BAG=45°，所以AB=
| 2 |
由圆锥曲线统一定义得：e=
| AF |
| AC |
| BF |
| BD |
∵|FB|=2|AF|，∴|BD|=2|AC|，
在直角梯形ABDC中，AG=BD-AC=AC，…②
由①、②可得AB=
| 2 |
又∵AF=
| 1 |
| 3 |
| ||
| 3 |
∴e=
| AF |
| AC |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考察了圆锥曲线的统一定义的应用，结合解含有45°的直角三角形，求椭圆的离心率，属于几何方法，运算量小，方便快捷．
练习册系列答案
名校课堂系列答案
相关题目
过椭圆左焦点F且倾斜角为60°的直线交椭圆于A，B两点，若|FA|=
|FB|，则椭圆的离心率等于（ ）
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|