题目内容
正四面体的四个顶点都在表面积为36π的一个球面上，则这个正四面体的高等于
4
4
．分析：画出几何图形，求出球的半径，即可求得正四面体的高．
解答：
解：正四面体内接于球，则相应的一个正方体内接于球
设正方体为ABCD-A1B1C1D1，则正四面体为ACB1D1
设球半径为R，则4πR2=36π，∴R=3
∴AC1=6，∴AD1=2
设底面ACB1中心为O，则AO=2
∴正四面体的高D1O=
=
=4
故答案为：4
解：正四面体内接于球，则相应的一个正方体内接于球设正方体为ABCD-A1B1C1D1，则正四面体为ACB1D1
设球半径为R，则4πR2=36π，∴R=3
∴AC1=6，∴AD1=2
| 6 |
设底面ACB1中心为O，则AO=2
| 2 |
∴正四面体的高D1O=
| AD12-AO2 |
| 24-8 |
故答案为：4
点评：本题考查正四面体与正方体的关系，在几何解题中，往往相互联系，本题中采用转化思想，把正四面体的高，棱长与正方体的棱长，外接球的直径相结合是关键．
练习册系列答案
相关题目
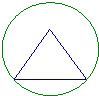棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
