题目内容
是否存在实数a,使得函数y=sin2x+acos x+ a-
a- 在闭区间
在闭区间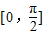 上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
【答案】分析:利用二倍角公式对函数解析式化简整理,进而利用x的范围确定cosx的范围,根据二次函数的性质对a的范围进行分类讨论,求得函数的最大值.
解答:解:y=1-cos2x+acosx+ a-
a-
=-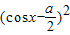 +
+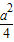 +
+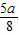 -
-
当0≤x≤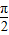 时,0≤cosx≤1,
时,0≤cosx≤1,
若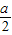 >1,即a>2,则当cosx=1时
>1,即a>2,则当cosx=1时
ymax=a+ a-
a- =1,
=1,
∴a=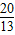 <2(舍去)
<2(舍去)
若0≤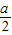 ≤1即0≤a≤2,则当cosx=
≤1即0≤a≤2,则当cosx=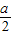 时,
时,
ymax=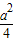 +
+ a-
a- =1,
=1,
∴a= 或a=-4(舍去).
或a=-4(舍去).
若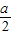 <0,即a<0时,则当cosx=0时,
<0,即a<0时,则当cosx=0时,
ymax= a-
a- =1,
=1,
∴a=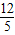 >0(舍去).
>0(舍去).
综上所述,存在a= 符合题设.
符合题设.
点评:本题主要考查了三角函数的求最值.考查了学生分析推理的能力,基础知识的掌握程度.
解答:解:y=1-cos2x+acosx+
 a-
a-
=-
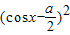 +
+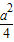 +
+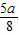 -
-
当0≤x≤
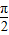 时,0≤cosx≤1,
时,0≤cosx≤1,若
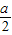 >1,即a>2,则当cosx=1时
>1,即a>2,则当cosx=1时ymax=a+
 a-
a- =1,
=1,∴a=
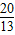 <2(舍去)
<2(舍去)若0≤
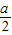 ≤1即0≤a≤2,则当cosx=
≤1即0≤a≤2,则当cosx=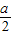 时,
时,ymax=
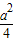 +
+ a-
a- =1,
=1,∴a=
 或a=-4(舍去).
或a=-4(舍去).若
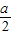 <0,即a<0时,则当cosx=0时,
<0,即a<0时,则当cosx=0时,ymax=
 a-
a- =1,
=1,∴a=
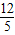 >0(舍去).
>0(舍去).综上所述,存在a=
 符合题设.
符合题设.点评:本题主要考查了三角函数的求最值.考查了学生分析推理的能力,基础知识的掌握程度.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目


 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.