题目内容
(本小题满分12分)已知函数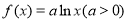 ,
,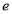 为自然对数的底数.
为自然对数的底数.
(1)过点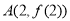 的切线斜率为
的切线斜率为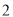 ,求实数
,求实数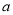 的值;
的值;
(2)当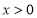 时,求证:
时,求证: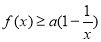 ;
;
(3)在区间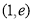 上
上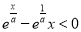 恒成立,求实数
恒成立,求实数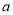 的取值范围.
的取值范围.
(1)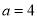 ;(2)详见解析;(3)
;(2)详见解析;(3)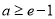 .
.
【解析】
试题分析:(1)求函数的导数,根据导数的几何意义即可求实数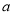 的值;(2)分析题意可知,问题等价于证明
的值;(2)分析题意可知,问题等价于证明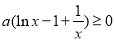 ,因此构造函数
,因此构造函数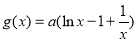 ,利用导数判断其单调性,通过求其最值即可证明;(3)将条件中的不等式参变分离,得
,利用导数判断其单调性,通过求其最值即可证明;(3)将条件中的不等式参变分离,得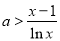 ,从而问题就等价于研究函数
,从而问题就等价于研究函数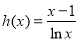 在区间
在区间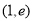 上的取值情况,利用导数判断其单调性即可求解.
上的取值情况,利用导数判断其单调性即可求解.
试题解析:(1) 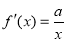 ,
,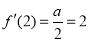 ,
,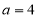 ; 2分
; 2分
(2)令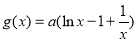 ,
,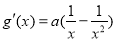 , 4分
, 4分
令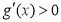 ,即
,即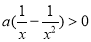 ,解得
,解得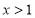 ,∴
,∴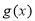 在
在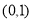 上递减,在
上递减,在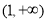 上递增,
上递增,
∴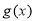 最小值为
最小值为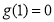 ,∴
,∴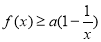 , 6分;(3)由题意可知
, 6分;(3)由题意可知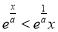 ,化简得
,化简得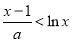 ,
,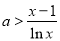 , 8分 令
, 8分 令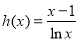 ,
,
则 ,
, , 9分
, 9分
由(2)知,在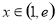 时,
时,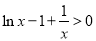 ,
,
∴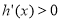 ,即
,即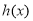 在
在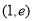 上单调递增,∴
上单调递增,∴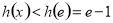 , 11分
, 11分
∴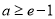 . 12分
. 12分
考点:1.利用导数研究曲线上某点切线方程;2.利用导数求函数的最值;3.恒成立问题.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 中,
中, 为边
为边 的中点,
的中点, ,
, ,分别以
,分别以 、
、 为圆心,
为圆心, 为半径作圆弧
为半径作圆弧 、
、 (
( 在线段
在线段 上).由两圆弧
上).由两圆弧 所围成的平面图形绕直线
所围成的平面图形绕直线 旋转一周,则所形成的几何体的体积为 .
旋转一周,则所形成的几何体的体积为 .
 的所有集合B的个数为( )
的所有集合B的个数为( ) ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 ,则
,则 的共轭复数
的共轭复数 ( )
( ) B.
B. C.
C. D.
D.
 中,若
中,若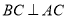 ,
,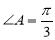 ,
,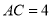 ,
,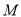 为
为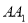 中点,点
中点,点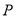 为
为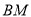 中点,
中点,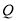 在线段
在线段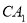 上,且
上,且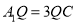 ,则异面直线
,则异面直线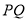 与
与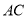 所成角的正弦值 .
所成角的正弦值 .
 ,
, 围成的封闭图形的面积为( )
围成的封闭图形的面积为( ) B.
B. C.
C. D.1
D.1 
 上与其焦点的距离等于
上与其焦点的距离等于 的点的坐标是 ;
的点的坐标是 ;