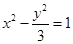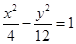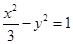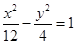题目内容
已知抛物线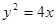 和点
和点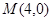 ,
, 为抛物线上的点,则满足
为抛物线上的点,则满足 的点
的点 有( )个。
有( )个。
A. | B.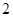 | C.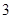 | D. |
A
解析试题分析:设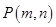
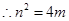
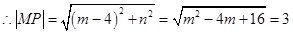
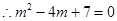
方程无解,所以点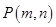 不存在
不存在
考点:抛物线方程及两点间距离
点评:两点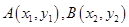 间距离
间距离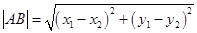

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知双曲线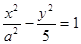 的右焦点为(3,0),则该双曲线的离心率等于 ( )
的右焦点为(3,0),则该双曲线的离心率等于 ( )
A.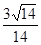 | B.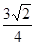 | C.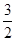 . . | D. |
已知双曲线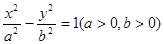 的渐近线与圆
的渐近线与圆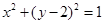 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )
A.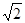 | B.2 | C.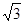 | D.3 |
设F为抛物线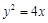 的焦点,
的焦点,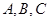 为抛物线上不同的三点,点
为抛物线上不同的三点,点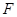 是△ABC的重心,
是△ABC的重心, 为坐标原点,△
为坐标原点,△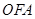 、△
、△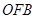 、△
、△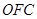 的面积分别为
的面积分别为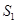 、
、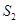 、
、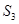 ,则
,则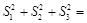 ( )
( )
| A.9 | B.6 | C.3 | D.2 |
顶点在原点,经过圆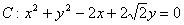 的圆心且准线与
的圆心且准线与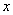 轴垂直的抛物线方程为
轴垂直的抛物线方程为
A.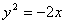 | B.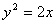 |
C.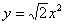 | D.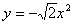 |
抛物线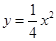 的焦点坐标是( )
的焦点坐标是( )
A.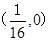 | B.(1,0) | C.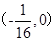 | D.(0,1) |
已知点P是以F1、F2为焦点的椭圆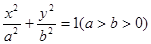 上一点,且
上一点,且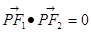 ,
,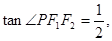 则该椭圆的离心率为( )
则该椭圆的离心率为( )
A.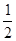 | B.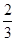 | C.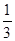 | D.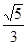 |
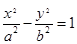 (
( )的两个焦点,若F1、F2、P(0,2
)的两个焦点,若F1、F2、P(0,2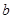 )是正三角形的三个顶点,则双曲线离心率是( )
)是正三角形的三个顶点,则双曲线离心率是( )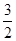
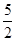
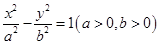 的两个焦点恰为椭圆
的两个焦点恰为椭圆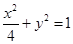 的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )
的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )