Question

（本题满分10分）

设多面体,已知,平面平面,△是以为斜边的等腰直角三角形,若，,为的

中点．

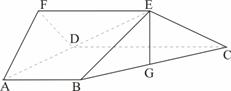（1）求证：平面；

（2）求直线与平面所成角的余弦值．

Answer 1

（1）证明：如图，设H是AD的中点，可得，则，又∵，

 ∴, 则为平行四边形,

故,则平面         4分

（2）解：∵△ADF是以AD为斜边的等腰直角三角形。

     ∴，又∵平面平面

     ∴平面，∴平面

     ∴是直线DE与平面ABCD所成的角   6分   ∵，∴，

又∵∴∴，又∵，由余弦定理

∴，，∴

又∵，∴  ，∴   …10分