题目内容
已知椭圆
+
=1(a>b>0)的左焦点为F,左、右顶点分别是A、C,上顶点为B,记△FBC外接圆为圆P.
(Ⅰ)判断直线AB和圆P能否相切?并说明理由;
(Ⅱ)若椭圆短轴长为2
,且椭圆上的点到F点最近距离为1,M、N是该椭圆上满足|OM|2+|ON|2=7的两点,求证:|kOM•kON|是定值,并求出此定值;
(Ⅲ)是根据(Ⅱ)的求解过程和结果,将命题进行推广,得到一个关于椭圆的一般性结论(无需证明).
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)判断直线AB和圆P能否相切?并说明理由;
(Ⅱ)若椭圆短轴长为2
| 3 |
(Ⅲ)是根据(Ⅱ)的求解过程和结果,将命题进行推广,得到一个关于椭圆的一般性结论(无需证明).
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)假设直线AB能与圆P相切,则kAB•kPB=-1,由此推导出c=2a,与0<c<a矛盾,从而线AB和圆P不能相切.
(Ⅱ)由a-c=1,2b=2
,得椭圆方程为
+
=1,由此利用点差法能证明|kOM•kON|是定值
.
(Ⅲ)由(Ⅱ)进行归纳整理,结合椭圆性质将命题进行推广,能得到一个关于椭圆的一般性结论
(Ⅱ)由a-c=1,2b=2
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 4 |
(Ⅲ)由(Ⅱ)进行归纳整理,结合椭圆性质将命题进行推广,能得到一个关于椭圆的一般性结论
解答:
(Ⅰ)解:由题意FC、BC的中垂直线方程公别为x=
,y-
=
(x-
),
∴圆心坐标为(
,
),
假设直线AB能与圆P相切,则kAB•kPB=-1,
∵kAB=
,kPB=
=
,
∴kAB•kPB=
=-1,
∴a2-c2+ac=a2-ac,
∴c2=2ac,又c>0,∴c=2a,
这与0<c<a矛盾,
∴线AB和圆P不能相切.
(Ⅱ)证明:由a-c=1,2b=2
,得a=2,b=
,
∴椭圆方程为
+
=1,
设M(x1,y1),N(x2,y2),由M,N在椭圆
+
=1上,
得
+
=1,
+
=1,
又|OM|2+|ON|2=7,∴x12+y12+x22+y22=7,
即x12+3(1-
x12)+x22+3(1-
x22)=7,即x12+x22=4,
∵|kOM•kON|=|
|=
=
=
=
,
∴|kOM•kON|是定值
.
(Ⅲ)解:一般性结论:已知椭圆
+
=1,(a>b>0),
M,N是该椭圆上满足|OM|2+|ON|2=a2+b2的两点,
则|kOM•kON|=
(定值).
| a-c |
| 2 |
| b |
| 2 |
| a |
| b |
| a |
| 2 |
∴圆心坐标为(
| a-c |
| 2 |
| b2-ac |
| 2b |
假设直线AB能与圆P相切,则kAB•kPB=-1,
∵kAB=
| b |
| a |
b-
| ||
0-
|
| b2+ac |
| b(c-a) |
∴kAB•kPB=
| b2+ac |
| a(c-a) |
∴a2-c2+ac=a2-ac,
∴c2=2ac,又c>0,∴c=2a,
这与0<c<a矛盾,
∴线AB和圆P不能相切.
(Ⅱ)证明:由a-c=1,2b=2
| 3 |
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
设M(x1,y1),N(x2,y2),由M,N在椭圆
| x2 |
| 4 |
| y2 |
| 3 |
得
| x12 |
| 4 |
| y12 |
| 3 |
| x22 |
| 4 |
| y22 |
| 3 |
又|OM|2+|ON|2=7,∴x12+y12+x22+y22=7,
即x12+3(1-
| 1 |
| 4 |
| 1 |
| 4 |
∵|kOM•kON|=|
| y1y2 |
| x1x2 |
|
|
=
| 3 |
| 4 |
|
| 3 |
| 4 |
∴|kOM•kON|是定值
| 3 |
| 4 |
(Ⅲ)解:一般性结论:已知椭圆
| x2 |
| a2 |
| y2 |
| b2 |
M,N是该椭圆上满足|OM|2+|ON|2=a2+b2的两点,
则|kOM•kON|=
| b2 |
| a2 |
点评:本题椭圆的标准方程的求法,考查两直线的斜率乘积的绝对值为定值的证明,考查命的推广,解题时要认真审题,注意点差数的合理运用.

练习册系列答案
相关题目
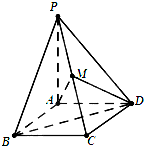 在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点.
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点.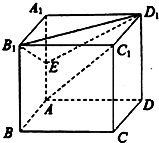 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中, 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.