题目内容
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的单调递增区间是( )
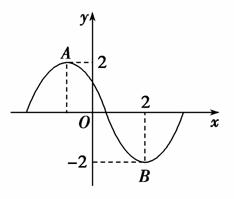
A.[6k-1,6k+2](k∈Z) B.[6k-4,6k-1](k∈Z)
C.[3k-1,3k+2](k∈Z) D.[3k-4,3k-1](k∈Z)
B
[解析] 由题意知AB=5,|yA-yB|=4,所以|xA-xB|=3,即 =3,所以T=
=3,所以T= =6,ω=
=6,ω=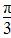 .由f(x)=2sin(
.由f(x)=2sin(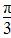 x+φ)过点(2,-2),得2sin(
x+φ)过点(2,-2),得2sin( +φ)=-2,0≤φ≤π,解得φ=
+φ)=-2,0≤φ≤π,解得φ=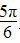 ,所以f(x)=2sin(
,所以f(x)=2sin(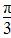 x+
x+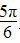 ),由2kπ-
),由2kπ- ≤
≤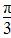 x+
x+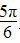 ≤2kπ+
≤2kπ+ (k∈Z),解得6k-4≤x≤6k-1(k∈Z),故函数f(x)的单调递增区间为[6k-4,6k-1](k∈Z).
(k∈Z),解得6k-4≤x≤6k-1(k∈Z),故函数f(x)的单调递增区间为[6k-4,6k-1](k∈Z).

练习册系列答案
相关题目
 +lg cosx的定义域是________________.
+lg cosx的定义域是________________.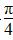 )的图象上各点的横坐标伸长到原来的3倍,再向右平移
)的图象上各点的横坐标伸长到原来的3倍,再向右平移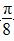 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )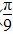 ,0) D.(
,0) D.(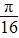 ,0)
,0)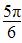 处取得最大值,则f(x)在[-π,0]上的单调增区间是( )
处取得最大值,则f(x)在[-π,0]上的单调增区间是( )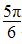 ] B.[-
] B.[-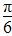 ]
]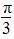 ,0] D.[-
,0] D.[- ,0)对称,则函数的解析式为________.
,0)对称,则函数的解析式为________.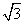 sinxcosx在区间[
sinxcosx在区间[ ,
, ]上的最大值是( )
]上的最大值是( )

 sinA,sinB),n=(cosB,
sinA,sinB),n=(cosB, B.
B. 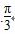
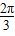 D.
D. 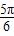
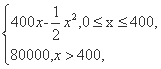 则总利润最大时,该门面经营的天数是 .
则总利润最大时,该门面经营的天数是 .