题目内容
如果对定义在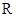 上的函数
上的函数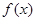 ,对任意两个不相等的实数
,对任意两个不相等的实数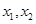 ,都有
,都有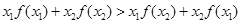 ,则称函数
,则称函数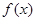 为“
为“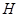 函数”.给出下列函数①
函数”.给出下列函数①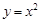 ;②
;②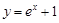 ;③
;③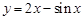 ;④
;④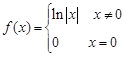 .以上函数是“
.以上函数是“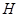 函数”的所有序号为 .
函数”的所有序号为 .
②③
解析试题分析: 即
即 ,
,
所以函数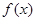 在
在 是增函数.
是增函数.
对于①,由 得
得 ,即函数在区间
,即函数在区间 是增函数,其不是“
是增函数,其不是“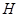 函数”;
函数”;
对于②,由由 恒成立,所以其为“
恒成立,所以其为“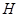 函数”;;
函数”;;
对于③,由 恒成立,所以其为“
恒成立,所以其为“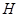 函数”;
函数”;
对于④,由于其为偶函数,所以其不可能在 是增函数.所以不是“
是增函数.所以不是“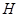 函数”.
函数”.
综上知,是“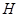 函数”的有②③.
函数”的有②③.
考点:函数的单调性,应用导数研究函数的单调性.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 满足
满足 ,且
,且 时,
时, ;函数
;函数 ,则函数
,则函数 与
与 的图象在区间
的图象在区间 内的交点个数共有 个.
内的交点个数共有 个. 对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与
轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与 轴交于点N(
轴交于点N( ),则
),则 ,记作
,记作

 ; ②
; ② ; ③
; ③ 是奇函数; ④
是奇函数; ④ (其中
(其中 为整数),则
为整数),则 最近的整数,记作
最近的整数,记作 ,即
,即 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题: 的定义域是
的定义域是 ,值域是
,值域是 ;
; 是
是 ;
; ;
; 上是增函数.
上是增函数.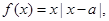 若对任意的
若对任意的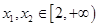 ,且
,且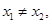
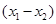
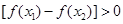 恒成立,则实数a的取值范围为 .
恒成立,则实数a的取值范围为 . 的反函数是
的反函数是  是定义在
是定义在 上的偶函数,在
上的偶函数,在 上是增函数,且
上是增函数,且 ,则使得
,则使得 的
的 的取值范围是_______.
的取值范围是_______.