题目内容
设函数
对任意
，都有
，且
> 0时，
< 0，
． （1）求
；
（2）若函数定义在
上，求不等式
的解集。
（1）f(0)=0 （2）
解析:
（1）令x=y=0,则f(0)= f(0)+ f(0) ∴f(0)=0
(2) 可先证明在R上是减函数。设
则
此时
∴
∴在R上是减函数 ，则在上也是减函数
等价于
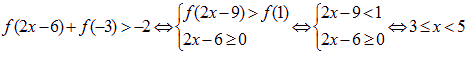
所不等式的解集为：
练习册系列答案
相关题目
解析:
题目内容
设函数对任意，都有，且> 0时，
< 0，． （1）求；
（2）若函数定义在上，求不等式的解集。
（1）f(0)=0 （2）
（1）令x=y=0,则f(0)= f(0)+ f(0) ∴f(0)=0
(2) 可先证明在R上是减函数。设 则 此时
∴
∴在R上是减函数 ，则在上也是减函数
等价于
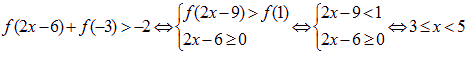
所不等式的解集为：
对任意
，都有
，当
时，
时 
，
对任意
，都有
，当
时，
时 
，
对任意
，都有
且
时，
．
上为减函数．
对任意实数
都有
且
时
。
内是增函数；
，试求
的取值范围。