题目内容
(2011•顺义区一模)已知函数f(x)=2sinxcosx+2
sin2x-
,(x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求f(x)的最大值,并指出取最大值时的x值.
| 3 |
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求f(x)的最大值,并指出取最大值时的x值.
分析:(Ⅰ)利用三角函数的恒等变换化简f(x)为2sin(2x-
),由此求出周期.
(Ⅱ)由于当2x-
=2kπ+
,k∈Z时,f(x)取得最大值,从而得到结论.
| π |
| 3 |
(Ⅱ)由于当2x-
| π |
| 3 |
| π |
| 2 |
解答:解:(Ⅰ)f(x)=2sinxcosx+2
sin2x-
=sin2x-
cos2x=2sin(2x-
),----(4分)
∴周期T=π.----(6分)
(Ⅱ)根据f(x)=2sin(2x-
),可得当2x-
=2kπ+
,k∈Z,即x=kπ+
时,----(10分)
f(x)max=2.----(13分)
| 3 |
| 3 |
| 3 |
| π |
| 3 |
∴周期T=π.----(6分)
(Ⅱ)根据f(x)=2sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
f(x)max=2.----(13分)
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域及周期性,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
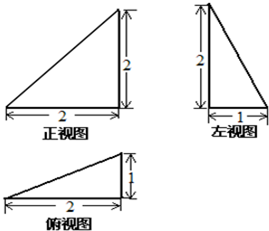 (2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )
(2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )